|
|
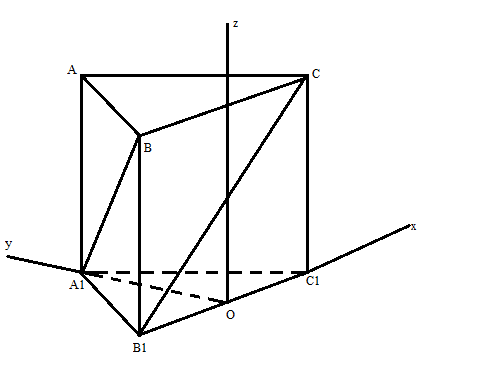
Gắn hệ trục tọa độ vào trong hình vẽ sao cho trung điểm O của $B_{1}C_{1}$ chính là gốc tọa độ, $OC_{1}$ trùng với Ox, $OA_{1}$ trùng với Oy, Oz vuông góc với mp ($A_{1}B_{1}C_{1}$) và cùng chiều với hình chóp
Khi đó tọa độ các điểm là: C(a/2, 0,a), B1(-a/2,0,0), B(-a/2,0 ,a), A1(0,$\frac{a\sqrt{3}}{2}$,0)
Khi đó, khoảng cách giưã $CB_{1}$ và $BA_{1}$ là: h= $\frac{\left| {\left[ {\overrightarrow{BA_{1}},\overrightarrow{CB_{1}}} \right]. \overrightarrow{BC}} \right|}{\left| {\left[ {\overrightarrow{CB_{1}},\overrightarrow{BA_{1}}} \right]} \right|}$ = $\frac{3a}{\sqrt{66}}$
|