Đặt $t = {5^x},t > 0$
$(1) \Leftrightarrow k{t^2} - t - k - 1 > 0\,\,\,\,(2)$
- Nếu $k = 0:\,\,\, - t - 1 > 0\,\, \Leftrightarrow t <  - 1$
$(2)$ không có nghiệm dương nên $(1)$ vô nghiệm.
- Nếu $k \ne 0\,:\,\,k{t^2} - t - k - 1 = 0\,\,\,\,$có $2$ nghiệm
                   $t =  - 1\,\,,\,\,\,t = 1 + \frac{1}{k}$
*Với $k > 0$có các nghiệm dương là $(1 + \frac{1}{k}, + \infty )\,$do đó $(1)$ có nghiệm.
*Với $k < 0$ ta có$f(t) > 0\,\, \Leftrightarrow \,\,{t_1} < t < {t_2}$
Để $(2)$ có nghiệm dương, điều kiện là  ${t_2} = 1 + \frac{1}{k} > 0 \Leftrightarrow k + 1 < 0$( vì $k < 0$) $ \Leftrightarrow k <  - 1$
Vậy với  $k <  - 1$hoặc $k > 0$ thì ($1)$ có nghiệm.

Đặt $t = {2^x},t > 0$ $(1)$ trở thành
${t^2} + mt + m - 1 \le 0$
$f(t) = {t^2} + mt + m - 1$ có $2$ nghiệm $\left[ \begin{array}{l}
t =  - 1\\
t =  - m + 1
\end{array} \right.$
- Nếu $ - m + 1 \le 0 \Leftrightarrow  m\ge 1\, \Rightarrow f(t)$có $2$ nghiệm âm nên$f(t) \le 0$ không có nghiệm dương nên $(1)$ vô nghiệm.
- Nếu $ - m + 1 > 0$ Khi đó $f(t) \le 0$ có tập các nghiệm dương là:$0 < t \le  - m + 1$ do đó $(1)$ có nghiệm.
       Vậy $\forall m < 1$thì $(1)$ có nghiệm.

Đặt $t = {5^x},t > 0$ ta có:
            $\,\,\,\,\,\,\,\,\,\,\,\,\,\,{t^2} - \left( {2m + 5} \right).t + {m^2} + 5 > 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall t > 0$
     Gọi $\,\,\,\,\,\,\,\,\,\,\,\,f(t) = \,\,{t^2} - \left( {2m + 5} \right).t + {m^2} + 5$
     Ta có $a = 1 > 0,\,\,\,\Delta  = {\left( {2m + 5} \right)^2} - 4\left( {{m^2} + 5} \right) = 25$
$f(t)$có $2$  nghiệm ${t_1},{t_2}$và $f(t) > 0$ có nghiệm là : $\left[ \begin{array}{l}
t < {t_1}\\
t > {t_2}
\end{array} \right.$
Để$\begin{array}{l}
f(t) > 0,\forall t > 0\,\,\,\, \Leftrightarrow \,\,\,{t_1} < {t_2} \le 0\\
 \Leftrightarrow \left\{ \begin{array}{l}
{\rm P} \ge 0\\
S < 0
\end{array} \right.\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left\{ \begin{array}{l}
{m^2} + 5 \ge 0\\
2m + 5 < 0
\end{array} \right.\,\,\,\,\,\,\,\, \Leftrightarrow m \le  - 5
\end{array}$

$\begin{array}{l}
(1) \Leftrightarrow \,\,\,\,\,0 < \sqrt 3 \sin \,2x - cos\,2x \le \sqrt 3 \\
\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\,0 < \frac{{\sqrt 3 }}{2}\sin \,2x - \frac{1}{2}cos\,2x \le \frac{{\sqrt 3 }}{2}\\
\,\,\,\,\,\,\, \Leftrightarrow 0 < \sin \left( {2x - \frac{\pi }{6}} \right) \le \sin \,\frac{\pi }{3}\\
\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}
k2\pi  < 2x - \frac{\pi }{6} \le \frac{\pi }{3} + k2\pi \\
\frac{{2\pi }}{3} + k2\pi  \le 2x - \frac{\pi }{6} < \pi  + k2\pi
\end{array} \right.\,\,\,\,\,\,\,\,\,\,,\,\,\,\,(k \in Z)\\
\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}
\frac{\pi }{{12}} + k\pi  < x \le \frac{\pi }{4} + k\pi \\
\frac{{5\pi }}{{12}} + k\pi  \le x < \frac{{7\pi }}{{12}} + k\pi
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,(k \in Z)
\end{array}$

Chia $2$ vế của $(1)$ cho ${4^{\frac{1}{x}}}$ta có :
 $\begin{array}{l}
x \ne 0\,\,\,\,\& \,\,(1) \Leftrightarrow 6{\left( {\frac{9}{4}} \right)^{\frac{1}{x}}} - 13{\left( {\frac{6}{4}} \right)^{\frac{1}{x}}} + 6 \le 0\\
 \Leftrightarrow 6{\left( {\frac{3}{2}} \right)^{2\left( {\frac{1}{x}} \right)}} - 13{\left( {\frac{3}{2}} \right)^{\frac{1}{x}}} + 6 \le 0
\end{array}$
 Đặt $t = {\left( {\frac{3}{2}} \right)^{\frac{1}{x}}},\,\,t > 0$  ta có :
$\begin{array}{l}
6{t^2} - 13t + 6 \le 0 \Leftrightarrow \frac{2}{3} \le t \le \frac{3}{2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {\frac{3}{2}} \right)^{ - 1}} \le {\left( {\frac{3}{2}} \right)^{\frac{1}{x}}} \le \frac{3}{2}x\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow  - 1 \le \frac{1}{x} \le 1\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}
x \le  - 1\\
x \ge 1
\end{array} \right.
\end{array}$

Với $\begin{array}{l}
a > 0,\,\,\,a \ne 1,\,\,{x^2} + ax + 5 \ge 0\\

\end{array}$
$(1) \Leftrightarrow {\log _a}3\left( { - {{\log }_3}\sqrt {{x^2} + ax + 5}  + 1} \right).{\log _5}\left( {{x^2} + ax + 6} \right) + 1 \ge 0$
$1)\,0 < a < 1:$
Đặt  $u = {x^2} + ax + 5,\,\,\,\,\,u \ge 0,$
$f(u){\log _3}\left( {\sqrt u  + 1} \right){\log _5}\left( {u + 1} \right) \ge 1$
Ta có   $f(4) = {\log _3}3.{\log _5}5 = 1$
$f(u)$là hàm tăng nên:$u \ge 4\,\,\,\, \Rightarrow f(u) \ge 1$
        ${x^2} + ax + 5 \ge 4 \Leftrightarrow {x^2} + ax + 1 \ge 0$
Vì $0 < a < 1:$nên ${a^2} - 4 < 0$
Bất phương trình không thỏa với $\forall x$
$\begin{array}{l}
2)\,a > 1:\,\,\,\,{\log _3}\left( {\sqrt u  + 1} \right){\log _5}\left( {u + 1} \right) \le 1\\
\,\,\,\,f(u) \le 1 \Rightarrow 0 \le u \le 4
\end{array}$
Từ đó: $\left\{ \begin{array}{l}
{x^2} + ax + 5 \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(a)\\
{x^2} + ax + 1 \le 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(q)
\end{array} \right.$
Xét $(b)$: $\left\{ \begin{array}{l}
\Delta  = {a^2} - 4\\
a > 1
\end{array} \right.$
  $a > 2:\,\,\,\,{x^2} + ax + 1$ có $2$ nghiệm
${x_1} = \frac{{ - a - \sqrt {{a^2} - 4} }}{2}$
${x_2} = \frac{{ - a + \sqrt {{a^2} - 4} }}{2}$
Suy ra $(a)$ $ \Leftrightarrow x_1^2 + a{x_1} + 5 = x_1^2 + a{x_1} + 1 + 4 = 4 > 0$
Tương tự $x_2^2 + a{x_2} + 5 > 0 \Rightarrow $với $a > 0$ thì bất phương trình không có nghiệm duy nhất.
Với $a = 2$ ta có $x =  - 1$
Vậy với $a = 2$ thì bất phương trình  có $1$ nghiệm duy nhất $x =  - 1$.

$(P)$ qua $C,\bot AH$ có PT :
$1.(x-3)+1.(y-2)-2(z-3)=0\Leftrightarrow  x+y-2z+1=0$
$B=(P)\cap BM,$ tọa độ $B$ thỏa mãn
$\begin{cases}x+y-2z+1=0 \\ x=1+t,y=4-2t,z=3+t \end{cases} $
$\Rightarrow  t+1+4-2t-6-2t+1=0$
$\Rightarrow  t=0\Rightarrow  B(1,4,3)$
- $(Q)$ qua $C,\bot  BM$ có PT :
$1.(x-3)-2(y-2)+1.(z-3)=0$
$\Leftrightarrow  x-2y+z-2=0$
- $K=(Q)\cap BM,$ tọa độ $K$ thỏa mãn :
$\begin{cases}x-2y+z-2=0 \\ x=1+t,y=4-2t,z=3+t \end{cases} \Rightarrow  t=1,K(2,2,4)$
- $E$ đối xứng với $C$ qua $K$, tọa độ $E$ xác định bởi :
$x_E=2x_K-x_C=1, y_E=2y_K-y_C=2, z_E=2z_K-z_C=5$
$\Rightarrow  E(1,2,5)$
- $A=BE\cap AH,PT$ của $BE :\begin{cases}x=1\\ y=4-t \\ z=3+t\end{cases}   $
Tọa độ $A$ thỏa mãn : $\begin{cases}x=1, y=4-t, z=3+t  \\ \frac{x-2}{1}=\frac{y-3}{1}=\frac{z-3}{-2}    \end{cases} \Leftrightarrow  \begin{cases}x=1 \\ y=2\\z=5 \end{cases} \Rightarrow  A(1,2,5)$
$AB=BC=CA=2\sqrt{2}\Rightarrow  \Delta ABC $ đều

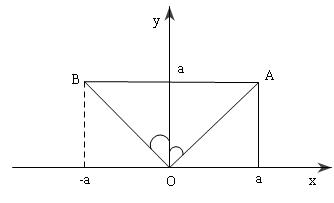Từ giả thiết ta có ngay $A(a;a;0)$;$B(-a;a;0)  $
Tứ diện $OABC$ có trọng tâm $G$ với tọa độ $G(0;\frac{a}{2};\frac{c}{4})$
Véc tơ $\overrightarrow {OG} (0;\frac{a}{2};\frac{c}{4})$
Mặt phẳng đi qua điểm $C(0;0;c)$ và vuông góc với đường thẳng đi qua $O$ và trọng tâm $G$ của tứ diện $OABC$ cũng là mặt phẳng qua $C(0;0;c)$ nhận $\overrightarrow u (0;\frac{a}{2};\frac{c}{4})$ là véc tơ pháp tuyến. Do đó mặt phẳng đã cho có pt: $2ay + cz – c^2 = 0$

$\sqrt {(x + 1)(4 - x)}  > x - 2          (1)$
TXĐ $-1\leq  x\leq  4$
- Với $-1\leq  x<2$ thì $x-2<0$ nên ($1$) đúng
- Với $2\leq  x\leq  4$ thì $x-2\geq  0$ nên
$(1)\Leftrightarrow  (x+1)(4-x)>(x-2)^2\Leftrightarrow  2x^2-7x<0\Leftrightarrow  0<x<\frac{7}{2} $
Kết hợp điều kiện $2\leq  x\leq  4\Rightarrow  2\leq  x<\frac{7}{2} $
Vậy $(1)$ có nghiệm là $-1\leq  x<\frac{7}{2} $

do giả thiết $0<C<90^0$ nên $cosC>0,$ do đó
(đpcm)$\Leftrightarrow  2cos3C-4cos2C+1\geq  2cosC$
Đặt $t=cosC$ thì điều kiện $0<A\leq  B\leq  C<90^0$
$\Rightarrow  60^0\leq  C<90^0\Rightarrow  0<t\leq  \frac{1}{2} $ và
(đpcm)$\Leftrightarrow  2(4t^3-3t)-4(2t^2-1)+1\geq  2t$
$\Leftrightarrow  (2t-1)[2t(2t-1)-5]\geq  0$
BĐT cuối đúng do $2t>0,2t-1\leq  0.$
Đẳng thức xảy ra $\Leftrightarrow  2t-1=0\Leftrightarrow  t=\frac{1}{2} $
$\Leftrightarrow  C=60^0\Leftrightarrow  \Delta ABC $ đều

$\sin 2x(cot x + tan2x) = 4cos^2x$
Điều kiện $\begin{cases}sinx\neq  0 \\ cos2x\neq  0 \end{cases} \Leftrightarrow \begin{cases} x\neq k\pi \\ x\neq \frac{\pi}{4}+\frac{k\pi}{2}\end{cases}, k\in Z$
Phương trình $\Leftrightarrow  sin2xcotx+sin2x.tan2x=4cos^2x$
$\Leftrightarrow  2cos^2x+\frac{sin^22x}{cos2x} =4cos^2x$
$\Leftrightarrow  \frac{1-cos^22x}{cos2x}=cos2x+1 $
$\Leftrightarrow  1-cos^22x=cos^22x+cos2x$
$\Leftrightarrow  2cos^22x+cos2x-1=0$
$\Leftrightarrow \begin{cases}cos2x=-1 \\ cos2x=\frac{1}{2}  \end{cases} $
$\Leftrightarrow  \begin{cases}2x=\pi+2k\pi \\ 2x=\pm\frac{\pi}{3}+2k\pi  \end{cases} \Leftrightarrow  \begin{cases}x=\frac{\pi}{2}+k \pi  \\ x=\pm\frac{\pi}{6}+k\pi  \end{cases}  (k\in Z)$ (thỏa mãn)

Xét $F(x)=f(x)-sinx$.Từ giả thiết, $F(x)$ liên tục trên $[0,\frac{\pi}{2} ],F(0)=f(0)-sin0=f(0)>0$
Lại có : $\int\limits_{0}^{\frac{\pi}{2} } (f(x)-sinx)dx<0\Rightarrow  \int\limits_{0}^{\frac{\pi}{2} } F(x)<0$
$\Rightarrow  \exists c\in [0,\frac{\pi}{2} ]$ để $F(c)<0$
Từ đó, $F(x)=0$ có nghiệm $x\in [0,c]\subset [0,\frac{\pi}{2} ]$