|
|
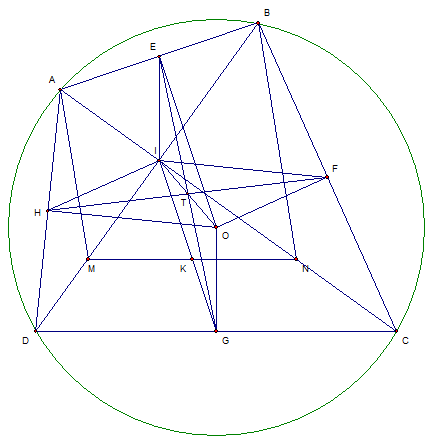
Dễ thấy $\Delta IAB\sim \Delta IDC$ nên $\frac{IA}{IB}=\frac{ID}{IC}$.
Trên đoạn $ID$ và $IC$ lấy điểm $M$ và $N$ sao cho $IM=IA$ và $IN=IB$.
Khi đó $\frac{IM}{IN}=\frac{IA}{IB}=\frac{ID}{IC}$ nên $MN//DC$.
Gọi $G,H,K$ là trung điểm $CD,DA,MN$ thì $K\in IG$.
Mặt khác $\Delta IAB=\Delta IMN$ nên tứ giác $ABNM$ nội tiếp. Mà $AB=MN$ nên $AM//BN$, suy ra tứ giác $ABNM$ là hình thang cân.
Theo giả thiết, $IE$ vuông góc với $CD$ nên $IE$ vuông góc với $MN$. Vì $ABNM$ là hình thang cân nên $IK$ vuông góc với $AB$, suy ra $IG$ vuông góc với $AB$.
Vì $O$ là tâm đường tròn ngoại tiếp tứ giác $ABCD$ nên $OE$ vuông góc với $AB$ và $OG$ vuông góc với $CD$. Từ đó suy ra $OE//IG$ và $OG//IE$ hay tứ giác $OEIG$ là hình bình hành.
Ta suy ra $OI$ cắt $EG$ tại trung điểm $T$ mỗi đường.
Dễ chứng minh tứ giác $EFGH$ là hình bình hành nên $EG$ và $FH$ cắt nhau tại trung điểm mỗi đường.
Ta được $OI$ và $FH$ cắt nhau tại trung điểm mỗi đường hay tứ giác $OFIH$ là hình bình hành.
Vậy $IF$ song song với $OH$, đồng thời vuông góc với $AD$.
|