a) Đặt $I_n=\int\limits_{0}^{1}x^n \sqrt{1-x}dx$
Trước hết chứng minh bổ đề  $I_n=\frac{2n}{2n+3}$. Bạn có thể sử dụng phương pháp tích phân từng phần để giải quyết coi như bài tập nhé.
Do $I_0=\frac{2}{3}$ và chú ý $\forall n$, ta có $\frac{1}{2n+1} < \frac{1}{\sqrt{2n(2n+2)}}$
$\implies I_n=\frac{2n}{2n+3}.\frac{2(n-1)}{2n+1}\cdots\frac{2}{5}.\frac{2}{3}<\frac{2n}{\sqrt{(2n+2)(2n+4)}}.\frac{2(n-1)}{\sqrt{2n(2n+2)}}\cdots\frac{2}{\sqrt{ 4.6}}.\frac{2}{\sqrt{2.4}}$
$\implies I_n<\frac{1}{(n+1)\sqrt{n+2}}<\frac{1}{(n+1)\sqrt{n+1}}$  (đpcm).

$I = \int\limits_3^5 {\sqrt {{x^2} - 9} dx} $
Đặt
$t = x + \sqrt {{x^2} - 9}  \Rightarrow x = \frac{{{t^2} + 9}}{{2t}} \Rightarrow dx = \frac{1}{2}\left( {1 - \frac{9}{{{t^2}}}} \right)dt$
và ta có
$I = \int\limits_3^9 {\left( {t - \frac{{{t^2} + 9}}{{2t}}} \right)\left( {\frac{1}{2}\left( {1 - \frac{9}{{{t^2}}}} \right)} \right)dt}  = \int\limits_3^9 {\left( {\frac{t}{4} - \frac{9}{{2t}} + \frac{{81}}{{4{t^3}}}} \right)dt}  = 10 - \frac{{9\ln 3}}{2}$

Tìm các hệ số $A,B,C,D$ bằng phương pháp đồng nhất thức
$ \frac{3x+1}{(x+1)^{3}x}dx =\frac{A}{(x+1)^3}+\frac{B}{(x+1)^2}+\frac{C}{x+1}+\frac{D}{x} $
ta được
$\begin{align*} \int\frac{3x+1}{(x+1)^{3}x}dx \ &=\int\frac{2}{(x+1)^3}-\frac{1}{(x+1)^2}-\frac{1}{x+1}+\frac{1}{x} \;dx \\ &=-\frac{1}{(x+1)^2}+\frac{1}{x+1}-\ln|x+1|+\ln |x|+C \\&= \ln|\frac{x}{x+1}|-\frac{1}{(x+1)^2}+\frac{1}{x+1}+C \\&=\ln|\frac{x}{x+1}|+\frac{x}{(x+1)^2}+C . \end{align*}$

b) Ta sẽ dùng phương pháp tích phân từng phần
Đặt $dv=\sin tdt$ và chọn $v=1-\cos t.$
$u=\frac1{t+1}\Rightarrow du=-\frac1{(t+1)^{2}}\,dt.$
Suy ra
$\int_{0}^{x}\frac{\sin t}{t+1}\,dt=\left.\frac{1-\cos t}{t+1}\right|_{0}^{x}-\int_{0}^{x}(1-\cos t)\left(-\frac1{(t+1)^{2}}\right)\,dt$

$=\frac{1-\cos x}{x+1}+\int_{0}^{x}\frac{1-\cos t}{(t+1)^{2}}\,dt$
Do $1-\cos x\ge 0$ $\forall x,$ nên cả hai tích phân đều không âm.
Từ đây có đpcm.

Từ giả thiết ta có $ \frac{n(n+1)}{2} +k = 202 $.
Do $ 1 \le k < n $ nên $ \begin{cases}\frac{n(n+1)}{2} \le 201 \\\frac{n(n+1)}{2} +n > 202  \end{cases}$$ \iff \begin{cases}n^2+n-402 \le 0 \\n^2+3n-404 > 0\end{cases}$$ \iff \begin{cases}n \le 19 \\n \ge 19\end{cases}$$ \iff n=19$.
Thay trở lại PT ban đầu ta được  $ \boxed{k = 12} $.

2. Ta có
$ (k+1)^2-k^2 = (k+1-k)(k+1+k)=(k+1)+k $
Do đó
$(2008)^2-(2007)^2+(2006)^2-(2005)^2+\ldots +2^2-1^2$
$ = 2008+2007+2006+2005+...+2+1 = \sum_{k=1}^{2008}k = \frac{2008.2009}{2}=2017036$.

3. $ [1+n(n+1)(n+2)(n+3)]^\frac{1}{2} =[1+(n^2+3n)(n^2+3n+2)]^\frac{1}{2}$

$=[(n^2+3n)^2+2.(n^2+3n)+1]^\frac{1}{2}=[(n^2+3n+1)^2]^\frac{1}{2}=n^2+3n+1
$

Ta có $ \frac{1}{a+b}= \frac{\sin^{4}x}{a}+\frac{\cos^{4}x}{b} \ge \frac{(\sin^2x+\cos^2x)^2}{a+b}=\frac{1}{a+b}$, do dấu bằng $\frac{\sin^{4}x}{a}+\frac{\cos^{4}x}{b} \ge \frac{(\sin^2x+\cos^2x)^2}{a+b}$ tương đương với $(b\sin^2x-a\cos^2x)\ge0$.
Ta suy ra $(b\sin^2x-a\cos^2x)=0.$ hay $\frac{\sin^2x}{a}=\frac{\cos^2x}{b}\implies\frac{\sin^2x}{a}=\frac{1-\sin^2x}{b}
\implies(a+b)(\sin^2x)=a \implies \sin^2x=\frac{a}{a+b}$.
do đó $\frac{\sin^2x}{a}=\frac{1}{a+b}$, và  $\frac{\cos^2x}{b}=\frac{1}{a+b}$.
tóm lại, $ \frac{\sin^{6}x}{a^{3}}+\frac{\cos^{6}x}{b^{3}}=
(\frac{\sin^2x}{a})^3+(\frac{\cos^2x}{b})^3=\boxed{\frac{2}{(a+b)^3}}$

Ảo thuật một chút nhé :)
       $\int\limits_{0}^{1} \frac{1+x.e^{2x}}{1+x.e^{x}} dx$
 $=\int\limits_{0}^{1} \frac{1+e^x+x.e^x+x.e^{2x}-e^x-x.e^x}{1+x.e^{x}} dx$
 $=\int\limits_{0}^{1} \frac{(1+e^x)(1+x.e^x)-(e^x+x.e^x)}{1+x.e^{x}} dx$
 $=\int\limits_{0}^{1} \left (1+e^x-\frac{e^x+x.e^x}{1+x.e^{x}} \right ) dx$
$=\int\limits_{0}^{1} (1+e^x)dx-\int\limits_{0}^{1}\frac{d(1+x.e^{x})}{1+x.e^{x}}$
 $=(x+e^x)|_0^1 - \ln(1+x.e^x)|_0^1$
 $=\boxed{e-\ln(1+e)}$

Bài tập này thực ra chỉ là một bài toán để mang đi đố vui. Vì tính chất của nó không thực sự phù hợp với toán cấp 3. Ở cấp học cao hơn, bạn sẽ có rất nhiều phương pháp để xử lý nó. Mình có thể giải chi tiết bài tập này, nhưng với phương pháp số phức. Còn nếu bạn muốn lời giải sơ cấp bằng phương pháp hạ bậc thì có lẽ mất vài ba trang giấy.
Mình sẽ đưa ra kết quả tổng quát cho bài này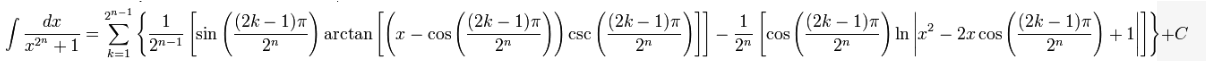

Sẽ là tốt hơn nếu bạn thử tập làm bài tập sau
Tìm nguyên hàm
$\int\limits_{}^{} \frac{1}{x^4+1} dx$

Kí hiệu $p$ là nửa chu vi của tam giác này.
$(a-b+c)\cot \frac{ C}{ 2} = (a+b+c) \tan \frac{A }{ 2} $
$\Leftrightarrow \frac{a-b+c}{a+b+c}=\tan \frac{A }{ 2}\tan \frac{C }{ 2}$
$\Leftrightarrow \frac{2p-2b}{2p}=\sqrt{\frac{(p-b)(p-c)}{p(p-a)}}.\sqrt{\frac{(p-b)(p-a)}{p(p-c)}}$
$\Leftrightarrow \frac{p-b}{p}=\frac{p-b}{p}$
như vậy đẳng thức này đúng với mọi tam giác $ABC$.

Bạn nên xem lại số liệu nhé. Bài sau có ích để tham khảo
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/113781/mot-bai-so-phuc-ma-trong-sach-k-co-dap-an

Viết lại đẳng thức cần chứn minh dưới dạng
$\sum \frac{ \tan A}{ \tan B \tan C} -\sum \tan A =-2 \sum \cot A       (1)$
Vế trái $(1) = \sum \tan A \left (  \frac{1}{ \tan B \tan C}-1 \right )= \sum \tan A \frac{1-\tan B \tan C}{ \tan B \tan C}$
$= \sum \tan A. \frac{1-\tan B \tan C}{ \tan B+ \tan C}.\frac{\tan B+ \tan C}{ \tan B \tan C}$
$= \sum \tan A. \frac{1}{\tan (B+C)}.\left (\frac{1}{ \tan B}+\frac{1}{ \tan C} \right )$
$= \sum \tan A. \frac{-1}{\tan A}.\left (\cot B+\cot C \right )$
$=-2 \sum \cot A  $     (đpcm)

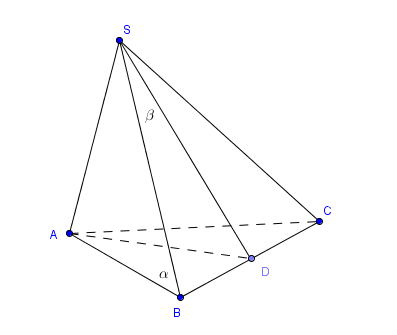Do $SA \perp (ABC) \implies \widehat{ABS}=\alpha$
Hai cạnh $SC, SB$ có các hình chiếu trên mp ABC là AB= AC. Nên SB=SC nên SBC là tam giác cân tại S. Lúc đó $SD \perp BC$. Cũng do $BD \perp AD$ nên $BD \perp (SAD) \implies \widehat{BSD}=\beta$.
Áp dụng tỉ số lượng giác ta có
$\frac{BD}{\sin \beta}=SB=\frac{BA}{\cos \alpha} \implies SB^2=\frac{BD^2}{\sin^2 \beta}=\frac{BA^2}{\cos^2 \alpha}=\frac{AD^2}{-\sin^2 \beta+\cos^2 \alpha}=\frac{a^2}{-\sin^2 \beta+\cos^2 \alpha}$
$\implies \begin{cases}SA=SB.\cos \alpha=\frac{a\cos \alpha}{\sqrt{-\sin^2 \beta+\cos^2 \alpha}} \\ S_{ABC}=AD.BD=\frac{a^2\sin \beta}{\sqrt{-\sin^2 \beta+\cos^2 \alpha}} \end{cases}$
Vậy $V=\frac{1}{3}SA.S_{ABC}=\frac{a^3\sin \beta\cos \alpha}{3(-\sin^2 \beta+\cos^2 \alpha)}$