Nếu đúng đề bài như thế này thì bài toán có duy nhất $1$ nghiệm. Nhưng không biểu diễn dưới dạng chính xác.
Ý tưởng trong lời giải này là sử dụng phương pháp giải bậc $4$ tổng quát.
Với điều kiện $\begin{cases}2t^2-3t-1 \ge 0 \\ t^2-1 \ge 0 \end{cases}\Leftrightarrow  t \ge \frac{3+ \sqrt{17}}{4}$
PT đã cho
$\Leftrightarrow 9(t^2-1)=(2t^2-3t-1)^2$
$\Leftrightarrow 4t^4-12t^3-4t^2+6t+10=0$
$\Leftrightarrow 4t^4-12t^3+9t^2=13t^2-6t-10$
$\Leftrightarrow \left[ {t(2t-3)} \right]^2=13t^2-6t-10$
Ta thêm vào tham số $a$ như sau,
$\Leftrightarrow \left[ {t(2t-3)} \right]^2+2a.t(2t-3)+a^2=(13+4a)t^2-6(a+1)t+a^2-10$
$\Leftrightarrow (2t^2-3t+a)^2=(13+4a)t^2-6(a+1)t+a^2-10      (*)$
Đặt $f(a)=(13+4a)t^2-6(a+1)t+a^2-10$. Bây giờ giả sử $a$ là số thỏa mãn
$\Delta'_f=9(a+1)^2-(13+4a)(a^2-10)=0\Leftrightarrow 4a^3+4a^2-58a-139=0       (**)$ (nếu có nghiệm đẹp thì PT này sẽ phải có nghiệm đơn giản)
Khi đó vế phải của PT $(*)$ có nghiệm duy nhất $t=\frac{3(a+1)}{3+2a}$. Và lúc đó
$\Leftrightarrow (2t^2-3t+a)^2=(13+4a)\left (t-\frac{3(a+1)}{3+2a} \right )^2           (***)$
Chú ý rằng ràng buộc $(**)$ là ràng buộc có nghĩa vì PT bậc $3$ luôn có nghiệm, và nghiệm này được chọn thỏa mãn $13+4a>0$.
Như vậy từ $(***)$ ta thu được hai PT bậc hai và có thể giải tiếp được.

Kí hiệu
$\prod \cos A = \cos A.\cos B.\cos C$,       
$\prod \cos(B-C)= \cos(A-B).\cos(B-C). \cos(C-A)$
BĐT cần chứng minh tương đương với
$\Leftrightarrow 8\prod \cos A \le \prod \cos(B-C)$
$\Leftrightarrow 8\prod (2\cos A\sin (B+C)) \le \prod 2\sin (B+C)\cos(B-C)$
$\Leftrightarrow 8\prod (2\cos A\sin A) \le \prod (\sin 2B + \sin 2C)$
$\Leftrightarrow 8\prod \sin 2A \le \prod (\sin 2B + \sin 2C)$
Do $A, B, C$ là các góc nhọn nên $\sin 2A, \sin 2B, \sin 2C >0$ do đó
$\prod (\sin 2B + \sin 2C) \ge \prod 2\sqrt{\sin 2B\sin 2C}= 8\prod \sin 2A $ (đpcm).
Đẳng thức xảy ra $\Leftrightarrow \triangle ABC$ đều.

Theo mình đề bài nên sửa thành như sau
 \[(x^2-6x+11)\sqrt{x^2-x+1}=2(x^2-4x+7)\sqrt{x-2}\]
Khi đó ta đặt $u=\sqrt{x^2-x+1}>0$ và  $v=\sqrt{x-2}>0$, thì PT đã cho trở thành:
\[(u^2-5v^2)u=(2u^2-6v^2)v \Leftrightarrow u^3-5uv^2=2u^2v-6v^3\]
Nếu $v=0$ thì $x=2$ không phải là nghiệm ta có thể đặt $t=\frac{u}{v}$ ,ta được \[t^3-2t^2-5t+6=0\]  và ta có $t=-2,1,3$
Với $t=-2$ là điều vô lý. ($u,v>0$)
Với $t=1 \Leftrightarrow u=v$ và $t=3 \Leftrightarrow u=3v$, thay trở lại $u,v$ ta được  $x=5\pm\sqrt{6}$.

Đặt $t = \tan \frac{x}{2}$.
PT $\Leftrightarrow \frac{2t}{1+t^2}+\frac{1-t^2}{1+t^2}=\frac{2t}{1-t^2}\Leftrightarrow t^4-4t^3-2t^2+1=0$
$\Leftrightarrow t^4-4t^3+4t^2=6t^2-1\Leftrightarrow \left[ {t(t-2)} \right]^2=6t^2-1$
Ta thêm vào tham số $a$ như sau,
$\Leftrightarrow \left[ {t(t-2)} \right]^2+2a.t(t-2)+a^2=(6+2a)t^2-4at+a^2-1$
$\Leftrightarrow (t^2-2t+a)^2=(6+2a)t^2-4at+a^2-1         (*)$
Đặt $f(a)=(6+2a)t^2-4at+a^2-1$. Bây giờ giả sử $a$ là số thỏa mãn
$\Delta'_f=4a^2-(6+2a)(a^2-1)=0\Leftrightarrow a^3+a^2-a-3=0       (**)$
Khi đó vế phải của PT $(*)$ có nghiệm duy nhất $t=-\frac{2a}{3+a}$. Và lúc đó
$\Leftrightarrow (t^2+t+a)^2=(6+2a)\left (t+\frac{2a}{3+a} \right )^2           (***)$
Chú ý rằng ràng buộc $(**)$ là ràng buộc có nghĩa vì PT bậc $3$ luôn có nghiệm, và nghiệm này được chọn thỏa mãn $6+2a>0$.
Như vậy từ $(***)$ ta thu được hai PT bậc hai và có thể giải tiếp được.

Bạn hãy tìm kiếm trước khi đăng bài nhé

http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/113652/bat-dang-thuc-dang-tong-quat

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Ta cần tìm hệ số của $x^{15}$ trong khai triển đa thức $P(x)$ dưới dạng $P(x)=a_0+a_1x+a_2x^2+\cdots+a_{20}x^{20}$. Nhận thấy rằng các số chứa $x^{15}$ chỉ nằm trong tổng
$15(1+x)^{15}+16(1+x)^{16}+\cdots+20(1+x)^{20}$.
Mặt khác theo khai triển Niu-tơn
$n(1+x)^n=n.\sum_{k=0}^{n}C_n^kx^k=\sum_{k=0}^{n}nC_n^kx^k$.
Như vậy, $a_{15}=15C_{15}^{15}+16C_{16}^{15}+17C_{17}^{15}+18C_{18}^{15}+19C_{19}^{15}+20C_{20}^{15}$.

$I=\int\limits_{1}^{e}\frac{3x\ln x+x+\ln x+3}{\sqrt{x\ln x+1} }dx $
$I=\int\limits_{1}^{e}\frac{2(x\ln x+1)+\ln x+x+\ln x+1}{\sqrt{x\ln x+1} }dx $
$I=\int\limits_{1}^{e}\left[ {2\sqrt{x\ln x+1}+\frac{(\ln x +1)(x+1)}{\sqrt{x\ln x+1} }} \right]dx $
$I=\int\limits_{1}^{e}\left[ {2\sqrt{x\ln x+1}+(x+1)\frac{\ln x +1}{\sqrt{x\ln x+1} }} \right]dx $
$I=\int\limits_{1}^{e}\left[ {2(x+1)'\sqrt{x\ln x+1}+(x+1)\sqrt{x\ln x+1}'} \right]dx $
$I=\int\limits_{1}^{e}\left[ {2(x+1)'\sqrt{x\ln x+1}+2(x+1)\sqrt{x\ln x+1}'} \right]dx $
$I=\int\limits_{1}^{e}\left[ {2(x+1)\sqrt{x\ln x+1}} \right]'dx $
$I= {2(x+1)\sqrt{x\ln x+1}} |_1^e $
$I=\boxed{\displaystyle{2\sqrt[3]{(1+e)^2}-4}} $

 

Đặt $x-y = a, x+y=b$. Ta biết rằng
$\begin{cases}x^2+y^2= \frac{a^2+b^2}{2}\\ xy= \frac{b^2-a^2}{4} \end{cases}$
Lúc đó HPT
$\Leftrightarrow \begin{cases} \frac{a^2+b^2}{2}=\frac{b^2-a^2}{4}+b \\ ab=3 \end{cases}$
$\Leftrightarrow \begin{cases} 3a^2+b^2-4b=0\\ a=\frac{3}{b} \end{cases}$
$\Leftrightarrow \begin{cases} \frac{27}{b^2} +b^2-4b=0\\ a=\frac{3}{b} \end{cases}$
$\Leftrightarrow \begin{cases} b^4-4b^3+27=0\\ a=\frac{3}{b} \end{cases}$
$\Leftrightarrow \begin{cases} (b-3)^2(b^2+2b+3)=0\\ a=\frac{3}{b} \end{cases}$
$\Leftrightarrow \begin{cases} b=3\\ a=1 \end{cases}$
$\Leftrightarrow \begin{cases} x=2\\ y=1 \end{cases}$

Ta có
$y ' = 12x^2(1-x)^2-8x^3(1-x)=4x^2(1-x)(3-5x)$
$y'=0 \Leftrightarrow \left[ {\begin{matrix} x=0\\x=1\\x=\frac{3}{5}  \end{matrix}} \right.$
$\begin{array}{c|ccccccccc}
x  &-\infty & \; & \; & 0 & \; & \; &  \frac{3}{5} & \; & \; &  1 & \; & \; &  +\infty \\
\hline
y'\;  & \; &+ \; & \; & \; 0 & \; & +\; & \; 0 \; & -\; & \: & 0  \; & &-\;  \\
\hline
\;  & \; & \; & \; & \;  & \; & \;  & \; \frac{432}{3125}& \;   \searrow & \: & \, & \nearrow & \, & +\infty  \\
\;  & \; & \; & \; & \; 0 & \; & \; & \; & \; & \: & 0    \\
y & \; & \; & \nearrow  &  \; & \; &   & \; &  \;&  \; & \; &   \\
\quad &  -\infty & \; & \; & \; & \; & \: &  & \; & \; & \; & \; & \: & \\

\end{array}$
Từ bảng biến thiên suy ra
Hàm số đạt cực tiểu tại $x=1; y=0$.
Hàm số đạt cực đại tại $x=\frac{3}{5}; y=\frac{432}{3125}$.

Ta sẽ chứng minh bất đẳng thức tổng quát sau
Cho $a, b, c, x, y, z$ là các số thực dương thì ta có
$abc+xyz \le \sqrt[3]{(a^3+x^3)(b^3+y^3)(z^3+c^3)}             (*)$
Thật vậy,
Áp dụng BĐT Cauchy cho các số dương ta được
$\displaystyle{\frac{3abc}{\sqrt[3]{(a^3+x^3)(b^3+y^3)(z^3+c^3)} }=3.\frac{a}{\sqrt[3]{a^3+x^3}}.\frac{b}{\sqrt[3]{b^3+y^3}}.\frac{c}{\sqrt[3]{c^3+z^3}} \le\frac{a^3}{a^3+x^3} +\frac{b^3}{b^3+y^3}+\frac{c^3}{c^3+z^3}}$
$\displaystyle{\frac{3xyz}{\sqrt[3]{(a^3+x^3)(b^3+y^3)(z^3+c^3)} }=3.\frac{x}{\sqrt[3]{a^3+x^3}}.\frac{y}{\sqrt[3]{b^3+y^3}}.\frac{z}{\sqrt[3]{c^3+z^3}} \le\frac{x^3}{a^3+x^3} +\frac{y^3}{b^3+y^3}+\frac{z^3}{c^3+z^3}}$
Cộng theo từng vế của hai BDDT trên ta được
$\displaystyle{\frac{3(abc+xyz)}{\sqrt[3]{(a^3+x^3)(b^3+y^3)(z^3+c^3)} } \le 3}$
Từ đây suy ra BĐT $(*)$ được chứng minh.

Đặt $a=|\sin m|, x=|\cos m|,b=|\sin n|, y=|\cos n|,c=|\sin p|, z=|\cos p|$.
Ta thấy rằng $0 \le a,b,c,x,y,z \le 1$ nên $0 \le a^3+x^3,b^3+y^3,z^3+c^3 \le 1$.
Chẳng hạn $0 \le a^3+x^3 \le a^2+x^2 =1$.
Sử dụng điều trên và áp dụng BĐT $(*)$ ta có
$\sin m \sin n \sin p + \cos m \cos n \cos p \le abc+xyz \le \sqrt[3]{(a^3+x^3)(b^3+y^3)(z^3+c^3)}  \le 1$. ĐPCM.

Câu $1$. PT

$\Leftrightarrow \tan (\pi \sin x)=\tan (\frac{\pi}{2}-\pi \cos x)$
$\Leftrightarrow \pi \sin x=\frac{\pi}{2}-\pi \cos x + k\pi         (k \in \mathbb{Z})$
$\Leftrightarrow  \sin x=\frac{1}{2}-\cos x + k        (k \in \mathbb{Z})$
 $\Leftrightarrow  \sin x=\frac{1}{2}-\cos x + k        (k \in \mathbb{Z})$
 $\Leftrightarrow  \sin x+\cos x=\frac{1}{2} + k        (k \in \mathbb{Z})$
 $\Leftrightarrow  \sqrt 2 \sin \left ( x +\frac{\pi}{4} \right )=\frac{1}{2} + k       (*) $
 Ta biết rằng $\left| {\sqrt 2 \sin \left ( x +\frac{\pi}{4} \right )} \right| \le \sqrt 2         \forall x.$  Do đó
 $\left| {\frac{1}{2} + k} \right| \le \sqrt 2$. Mà $k \in \mathbb{Z} \implies k \in \left\{ {-1; 0} \right\}.$
 + Với $k=0$. PT $(*)\Leftrightarrow  \sin \left ( x +\frac{\pi}{4} \right )=\frac{1}{2\sqrt 2} \Leftrightarrow \left[ {\begin{matrix} x=\arcsin\frac{1}{2\sqrt 2} -\frac{\pi}{4} +k2\pi \\x=\frac{3\pi}{4}-\arcsin\frac{1}{2\sqrt 2}  +k2\pi  \end{matrix}} \right. (k \in \mathbb{Z})$
+ Với $k=-1$. PT $(*)\Leftrightarrow  \sin \left ( x +\frac{\pi}{4} \right )=-\frac{1}{2\sqrt 2} \Leftrightarrow \left[ {\begin{matrix} x=\arcsin\frac{-1}{2\sqrt 2} -\frac{\pi}{4} +k2\pi \\x=\frac{3\pi}{4}-\arcsin\frac{-1}{2\sqrt 2}  +k2\pi  \end{matrix}} \right. (k \in \mathbb{Z})$

Mình vẫn cảm thấy mơ hồ về đề bài của bạn và không thể phác họa được hình vẽ theo các giả thiết như thế này.
Nếu đề bài vẫn như trên thì mình sẽ đưa ra lời giải như sau


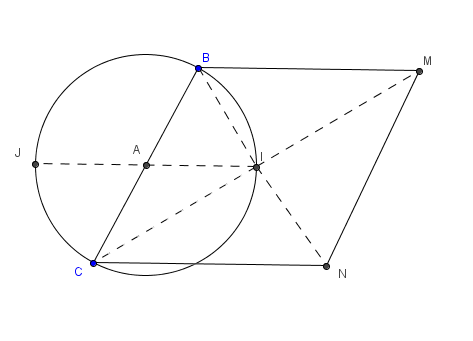
Xét PT tương giao
      $x^3-3x^2+mx+4-m=3-x$
$\Leftrightarrow x^3-x^2-2x^2+2x+(m-1)x-(m-1)=0$
$\Leftrightarrow (x-1)(x^2-2x+m-1)=0$
Dễ thấy hoành độ của $B,C$ là nghiệm của PT $x^2-2x+m-1=0     (*)  \Leftrightarrow (x-1)^2=2-m$
Từ đây ta phải có $m<2$ và $x_{B,C}=1 \pm \sqrt{2-m}$.
Thay trở lại PT của $(d)$ ta có
$B\left (1+ \sqrt{2-m}; 2- \sqrt{2-m} \right )$  và $C\left (1- \sqrt{2-m}; 2+ \sqrt{2-m} \right )$
 Và thấy rằng $A$ là trung điểm của $BC$ và $BC=2\sqrt{4-2m}$.
Vẽ đường tròn $(\alpha)$ tâm $A(1;2)$ đường kính $BC$ thì
$(\alpha) : (x-1)^2+(y-2)^2=4-2m$

Tiếp đến do $BMNC$ là hình thoi nên $BM \parallel CN \implies y'(x_B)=y'(x_C)$.
Do $y'=3x^2-6x+m \implies y'(x_B)=y'(x_C)=3-2m$
Qua $A$ vẽ đường thẳng song song với $BM, CN$ cắt đường tròn $(\alpha)$ tại $I$ thì $I$ chính là giao điểm hai đường chéo của hình thoi $BMNC$. Tọa độ của $I$ là nghiệm của hệ
$\begin{cases}(x-1)^2+(y-2)^2=4-2m \\ y=(3-2m)(x-1)+2 \end{cases}\Leftrightarrow I\left (1 \pm \sqrt{\frac{2-2m}{2m^2-6m+5}}; (3-2m)\left (\pm \sqrt{\frac{2-2m}{2m^2-6m+5}} \right )+2\right )$

Ta có $I$ là trung điểm của $BN, CM$
$\implies \begin{cases}N=(2x_I-x_B; 2y_I-y_B) \\ M=(2x_I-x_C; 2y_I-y_C) \end{cases}$
Từ đó tìm được tọa độ của $M,N$ theo $m$.
Do $M,N \in (C)$ nên ta thay tọa độ này vào PT của $(C)$ và tìm được $m$.