Bạn sẽ tìm được lời giải và nhiều vấn đề có liên quan tại đây
http://toan.hoctainha.vn/Thu-Vien/Chuyen-De/113302/ung-dung-tinh-don-dieu-cua-ham-so-de-chung-minh-bat-dang-thuc

Trước khi đăng đề bài bạn hãy sử dụng công cụ tìm kiếm nhé. Bài này chúng tôi đã thảo luận chi tiết tại đây
http://toan.hoctainha.vn/Hoi-Dap/Cau-Hoi/113597/ai-giai-giup-em-voi

Nếu đề bài của bạn là chính xác. Ta sẽ thực hiện như sau :
Đặt $t = \cos x \implies \begin{cases}\cos 2x=2t^2-1 \\ \cos 3x=4t^3-3t \\\cos 4x=2\cos^2 2x -1 = 8t^4-8t^2+1\end{cases}$
Nư vậy PT đã cho tương đương với
$\Leftrightarrow t(8t^4-8t^2+3)+2t^2-1-4t^3+3t=0$
$\Leftrightarrow 8t^5-12t^3+2t^2+6t-1=0$
 Kiểm tra được rằng phương trình này có một nghiệm duy nhất $t_0 \approx 0,166486$ và đa thức $8t^5-12t^3+2t^2+6t-1$ không thể phân tích thành tích của các đa thức hệ số thực có bậc nhỏ hơn $5$.
 Như vậy PT đã cho có nghiệm  $x= \pm \arccos t_0 + k2\pi \approx \pm \arccos0,166486 + k2\pi     (k \in \mathbb{Z}).$

Điều kiện : $\sin 2x \ne 0.$
Đặt $t= \tan \frac{x}{2}$ thì PT đã cho đương với
      $2\left ( \frac{1-t^2}{2t}-\frac{1-t^2}{1+t^2} \right )-3\left ( \frac{2t}{1-t^2}-\frac{2t}{1+t^2} \right )=1$
$\Leftrightarrow t^6-t^5-13t^4+4t^3-t^2-3t+1=0$
$\Leftrightarrow (t^2+3t-1)(t^4-4t^3-1)=0$
$\Leftrightarrow \left[ {\begin{matrix} t=\frac{1}{2}\left (-3 \pm \sqrt{13} \right )\Rightarrow x = 2k\pi +2\arctan\frac{1}{2}\left (-3 \pm \sqrt{13} \right )\\t^4-4t^3-1=0        (*)\end{matrix}} \right.$
PT $(*) \Leftrightarrow t^4-4t^3+4t^2=4t^2+1$
             $\Leftrightarrow \left[ {t(t-2)} \right]^2=4t^2+1$
             $\Leftrightarrow \left[ {t(t-2)} \right]^2-2t(t-2)+1=2t^2+4t+2$
             $\Leftrightarrow \left[ {t(t-2)-1} \right]^2=2(t+1)^2$
             $\Leftrightarrow\left[ {\begin{matrix}  t^2-2t-1-\sqrt 2 (t+1)=0\\  t^2-2t-1+\sqrt 2 (t+1)=0    \text {(vô nghiệm)}\end{matrix}}    \right.$   
             $\Leftrightarrow\left[ {\begin{matrix}  t=1+\frac{1}{\sqrt 2}+\sqrt{\frac{5}{2}+2\sqrt 2}\\ t=1+\frac{1}{\sqrt 2}-\sqrt{\frac{5}{2}+2\sqrt 2} \end{matrix}} \right.$     
 Đến đây bạn tự viết nốt nghiệm nhé.

Chúng ta đang bàn đến việc các nghiệm thực của PT.
Nhìn vào công thức $4$ nghiệm trên thì trước hết cần có $k^2-4 \ge 0 \Leftrightarrow |k| \ge 2.$
Để ý rằng muốn có $4$ nghiệm phân biệt thì các nghiệm $x_1,x_2,x_3,x_4$ phải đôi một khác nhau.
Ta có :
Hiển nhiên $x_1 \ne x_2$.
Giả sử $x_1 = x_3\Leftrightarrow -k+\sqrt{k^2+4}= k+\sqrt{k^2-4} \Leftrightarrow \sqrt{k^2+4}-\sqrt{k^2-4} = 2k $
$\Leftrightarrow \begin{cases}k \ge 0 \\ -\sqrt{k^4-16}=k^2\end{cases} \implies k^2+\sqrt{k^4-16}=0$, đây là điều không thể xảy ra. Vậy $x_1 \ne x_3$.
Giả sử $x_1 = x_4\Leftrightarrow -k+\sqrt{k^2+4}= k-\sqrt{k^2-4} \Leftrightarrow \sqrt{k^2+4}+\sqrt{k^2-4} = 2k $
$\Leftrightarrow \begin{cases}k \ge 0 \\ \sqrt{k^4-16}=k^2\end{cases} \implies k^4-16=k^4$, đây là điều không thể xảy ra. Vậy $x_1 \ne x_4$.
Tương tự ta cũng có : $x_2 \ne x_3, x_2 \ne x_4.$
Cuối cùng, giả sử $x_3 = x_4\Leftrightarrow k+\sqrt{k^2-4}= k-\sqrt{k^2-4} \Leftrightarrow \sqrt{k^2-4} = 0
\Leftrightarrow k=\pm 2$. Suy ra $x_3  \ne x_4 \Leftrightarrow k \ne \pm 2$.
Tổng hợp các kết quả ta có $|k|>2.$

Ta có
      $a\tan A+b\tan B=(a+b)\cot\frac{C}{2} $
$\Leftrightarrow a\tan A+b\tan B=(a+b)\tan\frac{A+B}{2} $
$\Leftrightarrow a\left (\tan A- \tan\frac{A+B}{2} \right )+b\left (\tan B- \tan\frac{A+B}{2} \right )=0$
$\Leftrightarrow \displaystyle{a\frac{\sin\frac{A-B}{2}}{\cos A \cos \frac{A+B}{2}}-b\frac{\sin\frac{A-B}{2}}{\cos B \cos \frac{A+B}{2}}}=0$
$\Leftrightarrow \left[ \begin{matrix} \sin\frac{A-B}{2}=0          (1)\\ \frac{a}{\cos A}-\frac{b}{\cos B}=0        (2)\end{matrix}\right.$
$(1)\Leftrightarrow A=B \Leftrightarrow \triangle ABC$ cân.
$(2)\Leftrightarrow\frac{a}{\cos A}=\frac{b}{\cos B}=0\Leftrightarrow \frac{a}{\frac{b^2+c^2-a^2}{2bc}}=\frac{b}{\frac{a^2+c^2-b^2}{2ac}} \Leftrightarrow b^2+c^2-a^2=a^2+c^2-b^2\Leftrightarrow a=b \Leftrightarrow \triangle ABC$ cân.

PT
$\Leftrightarrow x^4-(k^2x^2-2kx+1)=0$
$\Leftrightarrow x^4-(kx-1)^2=0$
$\Leftrightarrow (x^2+kx-1)(x^2-kx+1)=0$
$\Leftrightarrow \left[ {\begin{matrix} x^2+kx-1=0\\x^2-kx+1=0\end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x_1=\frac{1}{2}\left ( -k+\sqrt{k^2+4}\right )\\x_2=\frac{1}{2}\left ( -k-\sqrt{k^2+4}\right )\\x_3=\frac{1}{2}\left ( k+\sqrt{k^2-4}\right )\\x_4=\frac{1}{2}\left ( k-\sqrt{k^2-4}\right )\end{matrix}} \right.$
Từ đây nhận thấy với $|k| >2$ và  thì PT đã cho có $4$ nghiệm phân biệt.

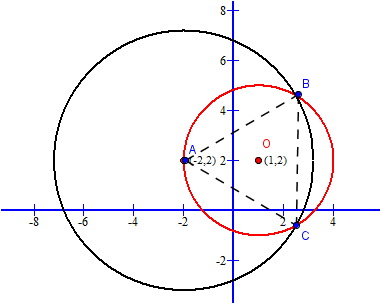Chúng ta còn một cách tiếp cận khác khi tìm ra
$(C): (x-1)^2+(y-2)^2=9 \Rightarrow (C)$ là đường tròn tâm $O(1,2)$, bán kính $3 $ và $A\in (C)$.
Tam giác đều $ABC$ nội tiếp đường tròn bán kính $R=3$ nên cạnh của tam giác đều là
$AB=AC=BC=R\sqrt 3= 3 \sqrt 3$  (bạn đọc tự lý giải điều này nhé.)
Lúc này $B, C$ là giao điểm của hai đường tròn tâm $O(1,2)$, bán kính $3 $ và đường tròn tâm $A(-2,2)$, bán kính $3\sqrt 3 $ nên tọa độ của $B, C$ là nghiệm của hệ
      $\begin{cases}(x-1)^2+(y-2)^2=9 \\ (x+2)^2+(y-2)^2=27 \end{cases} \Leftrightarrow \begin{cases}(x+2)^2-(x-1)^2=18 \\ (x+2)^2+(y-2)^2=27 \end{cases}$
$\Leftrightarrow \begin{cases}6x=15 \\ (x+2)^2+(y-2)^2=27 \end{cases}\Leftrightarrow \begin{cases}x=\frac{5}{2} \\ y=2\pm \frac{3\sqrt{3}}{2} \end{cases}$
Như vậy  $B\left(\frac{5}{2},2+ \frac{3\sqrt{3}}{2}\right);  C\left(\frac{5}{2},2- \frac{3\sqrt{3}}{2}\right)$.

Bài toán này còn có thể làm "chặt" bởi bất đẳng thức sau :
Cho tam giác $ABC$ nhọn.  Chứng minh rằng  $\sin A+\sin B+\sin C \le \frac{3 \sqrt 3}{2}$.
Trước hết ta chứng minh bài toán phụ sau,
Với $0< x,y < \frac{\pi}{2}$    thì    $\sin x + \sin y \le 2 \sin \frac{x+y}{2}$.
Thật vậy,
$\sin x + \sin y = 2 \sin \frac{x+y}{2} \cos \frac{x-y}{2} \le 2 \sin \frac{x+y}{2}$.
Đẳng thức xảy ra $\Leftrightarrow \cos \frac{x-y}{2}=1 \Leftrightarrow x=y.$
Bây giờ áp dụng BĐT này ta có
$\begin{cases}\sin A + \sin B \le 2 \sin \frac{A+B}{2}\\ \sin C + \sin \frac{\pi}{3} \le 2 \sin \frac{C+\frac{\pi}{3}}{2} \\ 2 \sin \frac{A+B}{2}+2 \sin \frac{C+\frac{\pi}{3}}{2}  \le 4 \sin \frac{A+B+C+\frac{\pi}{3}}{4}=4\sin\frac{\pi}{3} \end{cases}$
Cộng theo từng vế ba BĐT trên ta có
$\sin A+\sin B+\sin C \le 3\sin\frac{\pi}{3}=\frac{3 \sqrt 3}{2}$, đây là đpcm.
Đẳng thức xảy ra $\Leftrightarrow A=B=C \Leftrightarrow \triangle ABC$ đều.
Rõ ràng trong trường hợp này thì $\frac{3 \sqrt 3}{2} < \pi $ nên ta có kết luận của bài toán ban đầu.

Đặt $t=2^{\sin x}$ thì PT đã cho
$\Leftrightarrow t^2-2t \cos xy +2^{|y|}=0$
$\Leftrightarrow t^2-2t \cos xy +\cos^2 xy=\cos^2 xy-2^{|y|}$
$\Leftrightarrow \left ( t-\cos xy \right )^2=\cos^2 xy-2^{|y|}         (*)$.
Từ PT cuối này ta suy ra $\cos^2 xy \ge 2^{|y|} $.
Mặt khác  $\begin{cases}\cos^2 xy \le 1\\ 2^{|y|} \ge 1 \end{cases}        \forall x,y.$
Do đó ta phải có   $\cos^2 xy=2^{|y|}=1 \Leftrightarrow y=0$.
Lúc đó từ $(*) \Rightarrow t =\cos xy =1  $  (do $t>0$)  $\implies 2^{\sin x}=1 \implies \sin x=0 \implies x = k\pi  (k \in \mathbb{Z})$.
Vậy PT đã cho có nghiệm $(x;y)=(k\pi;0)   (k \in \mathbb{Z})$.

Ta sẽ dùng phương pháp tích phân từng phần để giải bài tập này

Đặt
$\begin{cases}u=\frac{1+\sin x }{1+\cos x } \\ dv=e^xdx \end{cases} \Rightarrow \begin{cases}du=\frac{1+\sin x+\cos x }{(1+\cos x)^2 } \\ v=e^x \end{cases} $.
Theo công thức TPTP, ta có
$I=\int\limits_{0}^{\frac{\pi}{2}}udv=uv |_0^{\pi/2}- \int\limits_{0}^{\frac{\pi}{2}}vdu=\frac{1+\sin x }{1+\cos x }. e^x |_0^{\pi/2} - \int\limits_{0}^{\frac{\pi}{2}}\frac{1+\sin x+\cos x }{(1+\cos x)^2 }. e^x dx$
$=2e^{\pi/2}-\frac{1}{2}-\int\limits_{0}^{\frac{\pi}{2}}\frac{ e^x }{1+\cos x} dx-\int\limits_{0}^{\frac{\pi}{2}}\frac{ e^x\sin x }{(1+\cos x)^2 } dx      (1)$
Với tích phân $I_1=\int\limits_{0}^{\frac{\pi}{2}}\frac{ e^x\sin x }{(1+\cos x)^2 } dx $ ta lại đặt
$\begin{cases}u=e^x \\ dv=\frac{ \sin x }{(1+\cos x)^2 } dx \end{cases} \Rightarrow \begin{cases}du=e^xdx \\ v=\frac{1}{1+\cos x} \end{cases} $.
Theo công thức TPTP, ta có
$I_1=\frac{e^x}{1+\cos x}|_0^{\pi/2}-\int\limits_{0}^{\frac{\pi}{2}}\frac{ e^x }{1+\cos x} dx =e^{\pi/2}-\frac{1}{2}-\int\limits_{0}^{\frac{\pi}{2}}\frac{ e^x }{1+\cos x} dx         (2)$
 Từ $(1)$ và $(2)$ suy ra $\boxed{I=e^{\pi/2}}$.

Ta có :
$y'=f'(x)= 2(m-1)\cos 2x + (4m+3)$
Đặt $t = \cos 2x \in [-1,1].$ thì $y'=g(t)=2(m-1)t+4m+3$
+ Nếu $m=1 \Leftrightarrow g(t)=7 > 0 \implies y' >0 \implies f $ đồng biến trên $\mathbb{R}.$
+ Nếu $m>1 \Leftrightarrow m-1>0  \implies g(t) $ đồng biến trên $ [-1,1].$
Do đó $\max_{ [-1,1]}g(t)=g(1)=6m+1$.
Để $f(x)$ đồng biến trên $\mathbb{R}$ thì $g(t)$ phải đồng biến trên $[-1,1]\Leftrightarrow \max_{ [-1,1]}g(t)=g(1)=6m+1 \ge 0 \Leftrightarrow m \ge -\frac{1}{6}$.
 Kết hợp với điều kiện $m>1$ thì ta được $f(x)$ đồng biến trên $\mathbb{R}$ nếu  $m>1$.
+ Nếu $m<1 \Leftrightarrow m-1<0  \implies g(t) $ nghịch biến trên $ [-1,1].$
Do đó $\max_{ [-1,1]}g(t)=g(-1)=2m+5$.
Để $f(x)$ đồng biến trên $\mathbb{R}$ thì $g(t)$ phải đồng biến trên $[-1,1]\Leftrightarrow \max_{ [-1,1]}g(t)=g(-1)=2m+5 \ge 0 \Leftrightarrow m \ge -\frac{5}{2}$.
 Kết hợp với điều kiện $m<1$ thì ta được $f(x)$ đồng biến trên $\mathbb{R}$ nếu  $1>m \ge -\frac{5}{2}$.

 Kết luận: $f(x)$ đồng biến trên $\mathbb{R}$ khi và chỉ khi $m \ge -\frac{5}{2}$.

Trước hết ta chứng minh BĐT phụ sau,  $\sin x < x    , \forall x>0.$
Thật vậy, xét hàm số $f(x)=\sin x - x$ thì $f'(x) = \cos x -1 < 0 , \forall x>0.$ tức là hàm số $f(x)$ nghịch biến trên $(0, + \infty).$
Từ đó với $x>0 \implies f(x) < f(0)=0 \implies \sin x - x < 0 \implies \sin x < x$ (đpcm).
Bây giờ áp dụng BĐT trên cho các góc $A, B, C >0$ thì ta có
$\begin{cases}\sin A < A \\ \sin B < B\\\sin C < C \end{cases} \implies \sin A+\sin B+\sin C <A+B+C=\pi$.

PT này vô nghiệm.

Ta sẽ chứng minh $10x^2+24y^2+8x+20y+51 > 0     \forall x,y.$
Thật vậy,
       $10x^2+24y^2+8x+20y+51$
$=\left ( \sqrt{10}x \right )^2 + 2. \sqrt{10}x.\frac{4}{ \sqrt{10}}+\frac{16}{10}+\left ( \sqrt{24}y \right )^2 + 2. \sqrt{24}y .\frac{10}{ \sqrt{24}}+\frac{100}{24}+\frac{1357}{30}$
 $=\left ( \sqrt{10}x+\frac{4}{ \sqrt{10}} \right )^2+\left (\sqrt{24}y+\frac{10}{ \sqrt{24}} \right )^2+\frac{1357}{30} > 0     \forall x,y.$

Chú ý rằng $\cos^{4}x-\sin^{4}x = \left ( \cos^{2}x-\sin^{2}x \right )\left (\cos^{2}x+\sin^{2}x \right )=\cos^{2}x-\sin^{2}x=\cos 2x$

Như vậy trước hết ta cần điều kiện $\cos 2x \ge 0.                      (1)$
Bây giờ PT đã cho $\Leftrightarrow \sin^{10}x\left (1-2\sin^{2}x \right )+\cos^{10}x\left (1-2\cos^{2}x \right )=\sqrt{2\cos 2x}$
                                 $\Leftrightarrow \sin^{10}x.\cos 2x-\cos^{10}x.\cos 2x=\sqrt{2\cos 2x}$
                                 $\Leftrightarrow \cos 2x\left ( \sin^{10}x-\cos^{10}x \right )=\sqrt{2\cos 2x}$
Từ đây suy ra
$\sin^{10}x-\cos^{10}x \ge 0 \Leftrightarrow \sin^{10}x \ge \cos^{10}x\Leftrightarrow |\sin x| \ge |\cos x|\Leftrightarrow \sin^{2}x \ge \cos^{2}x \Leftrightarrow \cos^{2}x - \sin^{2}x \le 0 \Leftrightarrow \cos 2x \le 0                (2)$.
Từ $(1)$ và $(2)$ suy ra $\cos 2x = 0 \Leftrightarrow x = \frac{\pi}{4}+\frac{k\pi}{2}   (k\in \mathbb{Z}).$