|
|
giải đáp
|
kho` qua
|
|
|
|
Ta có \(I = \int\limits_0^{\pi /2} {\left[ {\left( {1 + \cos x}
\right).\ln \left( {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}} \right) -
\ln \left( {1 + \cos x} \right)} \right]} dx\)
\( =
\int\limits_0^{\pi /2} {\cos x\ln \left( {1 + {\mathop{\rm s}\nolimits}
{\rm{inx}}} \right)dx + } \int\limits_0^{\pi /2} {\ln \left( {1 +
{\mathop{\rm s}\nolimits} {\rm{inx}}} \right)dx - } \int\limits_0^{\pi
/2} {\ln \left( {1 + \cos x} \right)dx} \)
Đặt \(t = \frac{\pi }{2} - x \)
$\Rightarrow
\int\limits_0^{\pi /2} {\ln \left( {1 + {\mathop{\rm s}\nolimits}
{\rm{inx}}} \right)dx= \int\limits_{\pi /2}^0 { - \ln \left( {1 + \cos
t} \right)dt= }}\int\limits_0^{\pi /2} {\ln \left( {1 + \cos t}
\right)dt )\\
\Rightarrow I = \int\limits_0^{\pi /2} {\cos x.\ln \left( {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}} \right)dx} } \\
=
\int\limits_0^{\pi /2} {\ln \left( {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}} \right)d(1+\sin x)} $
Đặt $t$ = \(\left( {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}} \right)\)
thì \(I = \int\limits_1^2 {\ln t dt =(t\ln t-t)|^{2}_{1}= 2\ln 2 - 1}
\) , (áp dụng tích phân từng phần).
|
|
|
|
giải đáp
|
chém hộ em
|
|
|
|
Gợi ý: $\frac{1}{x(x+1)^2} =\frac{1}{x}-\frac{1}{x+1}-\frac{1}{(x+1)^2}$ |
|
|
|
|
|
giải đáp
|
Giới hạn của hàm số lượng giác~ help me!
|
|
|
|
$\mathop {\lim }\limits_{x \to 0}\frac{\cos \left ( \frac{\pi }{2}\cos x \right )}{\sin \left ( \tan x \right )}=\mathop {\lim }\limits_{x \to 0}\frac{\sin \left ( \frac{\pi }{2}-\frac{\pi }{2}\cos x \right )}{\sin \left ( \tan x \right )}=\mathop {\lim }\limits_{x \to 0}\frac{\sin \left ( \pi\sin^2 \frac{x}2 \right )}{\sin \left ( \tan x \right )}$ $=\mathop {\lim }\limits_{x \to 0}\pi.\frac{\sin \left ( \pi\sin^2 \frac{x}2 \right )}{ \pi\sin^2 \frac{x}2}.\frac{\sin^2 \frac{x}2}{\frac{x^2}4}.\frac14.\frac{\tan x}{\sin \left ( \tan x \right )}.\frac{x}{\tan x}.x =\pi.1.1.\frac14.1.1.0=0$ |
|
|
|
giải đáp
|
Nguyên hàm của hàm lượng giác
|
|
|
|
4. Xét : $F(x)=\int\limits \frac{\sin x}{1+\sin
2x}dx=\frac{1}{2}\int\limits \frac{(\sin x+\cos x)-(\cos x-\sin
x)}{(\sin x+\cos x)^2}dx $
$=\frac{1}{2}\int\limits \frac{dx}{\sin x+\cos x}-\frac{1}{2}\int\limits \frac{(\cos x-\sin x)dx}{(\sin x+\cos x)^2} $
Tính
: $I_1= \frac{1}{2}\int\limits \frac{dx}{\sin x+\cos x} $.Đặt $t=\tan
\frac{x}{2} \Rightarrow dx=\frac{2dt}{1+t^2}; \sin x+\cos
x=\frac{-t^2+2t+1}{1+t^2} $
Lúc đó : $I_1 =\frac{1}{2}\int\limits
\frac{2dt}{-t^2+2t+1}=\frac{1}{4 {\sqrt{2}} }\int\limits (\frac{1}{t-1-
{\sqrt{2}} }- \frac{1}{t-1+ {\sqrt{2}} } )dt $
$ \Rightarrow {I_1}
= \frac{1}{{4\sqrt 2 }}\ln \left| {\frac{{t - 1 - \sqrt 2 }}{{t - 1 +
\sqrt 2 }}} \right| + {C_1} = \frac{1}{{4\sqrt 2 }}\ln \left|
{\frac{{\tan \frac{x}{2} - 1 - \sqrt 2 }}{{\tan \frac{x}{2} - 1 + \sqrt 2
}}} \right| + {C_1}\,\,(1)$
Tính : $I_2=\frac{1}{2}\int\limits
\frac{(\cos x-\sin x)dx}{(\sin+\cos x)^2}=\frac{1}{2} \int\limits
\frac{d(\cos x+\sin x)}{(\cos x+\sin x)^2}=-\frac{1}{2}\frac{1}{\sin
x+\cos x}+C_2 (2) $
Từ $(1) và (2) $ :
$F(x)=
\frac{1}{{4\sqrt 2 }}\ln \left| {\frac{{\tan \frac{x}{2} - 1 - \sqrt 2
}}{{\tan \frac{x}{2} - 1 + \sqrt 2 }}} \right|+\frac{1}{2}\frac{1}{\sin
x+\cos x}+ C $
Trong đó $C=C_1-C_2 :$ là hằng số tùy ý
|
|
|
|
giải đáp
|
Phương trình và bất phương trình.
|
|
|
|
3. TXĐ: $\left\{ \begin{array}{l}
1 - 4{x^2} \ge 0\\
x \ne 0
\end{array} \right.$
$ \bullet - \frac{1}{2} \le x < 0 \Rightarrow 1 - 4{x^2} < 0$ $ \Rightarrow 1 - \sqrt {1 - 4{x^2}} > 0 \Rightarrow \frac{{1 - \sqrt {1 - 4{x^2}} }}{x} < 0 (1)$ đúng $\bullet 0 < x \le \frac{1}{3} \Rightarrow 1 - 3x < 0 \Leftrightarrow (1)$ đúng $\bullet \frac{1}{3} < x \le \frac{1}{2} \Rightarrow 1 - 3x > 0$ $\begin{array}{l}
(1) \Leftrightarrow {(1 - 3x)^2} < 1 - 4{x^2} \Leftrightarrow 13{x^2} - 6x < 0\\
\Leftrightarrow 13x\left( {x - \frac{6}{{13}}} \right) < 0\forall x \in (\frac{1}{3};\frac{1}{2}{\rm{]}}
\end{array}$
Vậy ($1$) đúng $\forall x \in [ - \frac{1}{2};0{\rm{)}}\bigcup$ $(0;\frac{1}{2}{\rm{]}}$ |
|
|
|
giải đáp
|
Mong mọi người giúp mình
|
|
|
|
2. 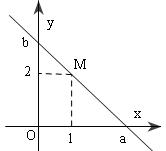 Vì $d$ cắt $(Ox), (Oy)$ nên phương trình $d$ có dạng : $\frac{x}{a} +\frac{y}{b} =1$ $d$ qua $M(1,2) : \frac{1}{a}+\frac{2}{b} =1 (*)$ Trường hợp một : $a=b\neq 0$ $(*)\Rightarrow \frac{1}{b}+\frac{2}{b}=1\Leftrightarrow b=3=a $ $\Rightarrow d : \frac{x}{3}+\frac{y}{3}=1 $ hay $x+y-3=0$ Trường hợp hai : $a=-b\neq 0$ $(*)\Rightarrow \frac{1}{-b}+\frac{2}{b}=1\Rightarrow b=1; a=-1 $ $\Rightarrow d : \frac{x}{-1}+\frac{y}{1}=1 $ hay $x-y+1=0$ Trường hợp $3: d$ qua $O(0,0),M(1,2)$ $d\equiv OM : \frac{y-y}{y_M-y_0}=\frac{x-x_0}{x_M-x_0} $ $\Rightarrow d : \frac{y}{2} =\frac{x}{1} $ hay $y=2x$ hay $2x-y=0$ |
|
|
|
giải đáp
|
Giúp với!!!!!!!!!!
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
mọi người giúp với
|
|
|
|
a. $|2\sin n + 3\cos n| \le 2|\sin n|+3|\cos n|=5$. Suy ra $-\frac{5}{n^2+1} \le \frac{2\sin n + 3\cos n}{n^2+1} \le \frac{5}{n^2+1}$. Mặt khác $\lim \frac{5}{n^2+1} = \lim\left ( - \frac{5}{n^2+1} \right )=0\Rightarrow \lim \frac{2\sin n + 3\cos n}{n^2+1}=0.$ |
|
|
|
|
|
giải đáp
|
cấp số nhân
|
|
|
|
Sử dụng $ b^2=ac$ ta có:
b) ĐT $\Leftrightarrow a^2b^2+b^2c^2+a^2c^2+b^4=a^2b^2+b^2c^2+2a^2c^2$ (Đúng)
a) ĐT $\Leftrightarrow (ab+b^2+bc)^3=b.b^2(a+b+c)^3$
$\Leftrightarrow b^3(a+b+c)^3=b^3(a+b+c)^3$ (Đúng)
|
|
|
|
giải đáp
|
help me
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
|
|
giải đáp
|
Giải hệ: \begin{cases}3(x^3 -y^3)=4xy \\ x^2 y^2= 9\end{cases}
|
|
|
|
Gợi ý: Từ PT thứ hai $\Leftrightarrow xy=\pm 3$. + Nếu $xy=3$. Biến đổi PT thứ nhất $\Leftrightarrow 3(x-y)(x^2+y^2+xy)=12\Leftrightarrow (x-y)((x-y)^2+3xy)=4$ $\Leftrightarrow (x-y)^3+9(x-y)-4=0$ Đây là PT bậc 3 theo $x-y$ có một nghiệm thực nhưng không đẹp, phải dùng công thức nghiệm bậc ba tổng quát Cardano để giải quyết. + Nếu $xy=-3$. Biến đổi PT thứ nhất $\Leftrightarrow 3(x-y)(x^2+y^2+xy)=-12\Leftrightarrow (x-y)((x-y)^2+3xy)=-4$ $\Leftrightarrow (x-y)^3-9(x-y)+4=0$ Đây là PT bậc 3 theo $x-y$ có ba nghiệm thực nhưng không đẹp, phải dùng công thức nghiệm bậc ba tổng quát Cardano để giải quyết. |
|
|
|
giải đáp
|
giải hệ: \begin{cases}y^2+x=x^2 +y \\ 2^{x}= 3^{y+1}\end{cases}
|
|
|
|
Gợi ý: Từ PT thứ nhất $\Leftrightarrow (x-y)(x+y-1)=0$. + Nếu $x=y$ thay vào Pt thứ hai $\Leftrightarrow 2^y=3^{y+1}\Leftrightarrow y\ln 2=(y+1)\ln3$ $\Leftrightarrow y(\ln 2 - \ln 3)=\ln 3\Leftrightarrow x=y=\frac{\ln 3}{\ln 2 - \ln 3}$. + Nếu $x=1-y$ thay vào Pt thứ hai $\Leftrightarrow 2^{1-y}=3^{y+1}\Leftrightarrow (1-y)\ln 2=(y+1)\ln3$ $\Leftrightarrow y(\ln 2 + \ln 3)=\ln 2-\ln 3\Leftrightarrow x=y=\frac{\ln 2-\ln 3}{\ln 2 + \ln 3}$. |
|