Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Ta có $y'=4x^3-4x(m^2-m+1)$.
Chú ý rằng $m^2-m+1 > 0          \forall m $.
Do đó $y'=0 \Leftrightarrow \left[ {\begin{matrix} x_1=0\\ x_2=\sqrt{m^2-m+1} \\ x_3=-\sqrt{m^2-m+1} \end{matrix}} \right.$
Nhận thấy $A(x_2;y_2), B(x_3;y_3)$ là các điểm cực tiêu của hàm số, và thay $x_2, x_3$ vào PT hàm số ta tìm được
$y_2=y_3=m-1-(m^2-m+1)^2$
Ta có $AB^2=(x_2-x_3)^2+(y_2-y_3)^2=4(m^2-m+1)=(4m^2-4m+1)+3 = (2m-1)^2+3 \ge    \forall m $.
Do đó $\min AB= \sqrt 3 \Leftrightarrow m=\frac{1}{2}$.

$\left\{ \begin{array}{l} x^2y^2-2x+y^2=0    (1)\\ 2x^2-4x+3+y^3=0    (2)\end{array} \right.$
 Từ PT $(2)\Leftrightarrow 2x^2-4x+2=-1-y^3\Leftrightarrow 2(x-1)^2=-1-y^3$
 Nhận thấy rằng $(x-1)^2 \ge 0     \forall x \implies -1-y^3 \ge 0 \implies y^3 \le -1 \implies y \le -1 \implies y^2 \ge 1$.
 Từ đây suy ra $x^2y^2-2x+y^2 \ge x^2-2x+1=(x-1)^2 \ge 0 $.
Tức là , $x^2y^2-2x+y^2 \ge 0$. Mặt khác thì PT $(1)$ xảy ra nên ta phải có $x=1, y=-1$. Đây cũng là nghiệm duy nhất của HPT.

Trước hết thấy rằng $(C)$ là đường tròn tâm $I(2;-1)$ bán kính $R=2$.
Để $MN$ là tiếp tuyến của $(C)$ thì khoảng cách từ $I$ đến đường thẳng $MN$ phải bằng bán kính của $(C)$.
Tiếp theo viết phương trình đường thẳng đi qua hai điểm $M, N$. Có hai trường hợp
+ $m=n \implies (MN) : x=m $. Khoảng cách $h$ từ $I$ đến đường thẳng $MN$ được tính bởi công thức
$h=|2-m|$. Ta cần có $h=R=2\Leftrightarrow |2-m|=2\Leftrightarrow \left[ {\begin{matrix} m=n=4\\ m=n=0 \end{matrix}} \right.$
+ $m \ne n \implies (MN) : \frac{x-n}{m-n}=\frac{y-0}{3-0}\Leftrightarrow (m-n)y-3x+3n=0 $. Khoảng cách $h$ từ $I$ đến đường thẳng $MN$ được tính bởi công thức
$h=\frac{|n-m-6+3n|}{\sqrt{(m-n)^2+3^2}}$. Ta cần có $h=R=2\Leftrightarrow\frac{|4n-m-6|}{\sqrt{(m-n)^2+9}}=2.$

Viết lại phương trình đã cho dưới dạng    $x^3-6x^2=-m            (*)$.
Bây giờ hãy khảo sát sự biến thiên và vẽ đồ thị hàm số $y=x^3-6x^2$. Thao tác chi tiết bạn hãy tập làm nhé, mình xin đưa ra kết quả là bảng biến thiên như sau
$\begin{array}{c|ccccccccc}
x  &-\infty & \; & \; & 0 & \; & \; &  4 & \; & \; &  +\infty \\
\hline
y' & \; &+ & \; & 0 & \; & - &  0 & \; & + & \; & \\
\hline
\;  & \; & \; & \; & \; 0 & \; & \; & \; & \; & \: & +\infty    \\
y & \; & \; & \nearrow  &  \; & \; &  \searrow & \; &  \;  \nearrow \\
\quad & -\infty & \; & \; & \; & \; & \: & -32
\end{array}$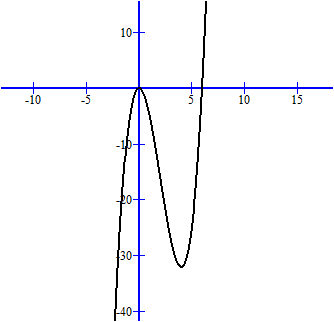




Nhìn vào bảng biến thiên và đồ thị, chú ý rằng PT $y=-m$ là những đường thẳng song song với trục hoành, vì thế để PT $(*)$ có ba nghiệm phân biệt thì $-32<-m<0 \Leftrightarrow 0<m<32.$

Bạn đọc tự chứng minh công thức sau coi như bài tập nhé.
$\cot 2x - \tan 2x = 2\cot 4x$
Với điều kiện $\sin 2x, \cos 2x, \sin 3x \ne 0 $ thì
PT $\Leftrightarrow (\cot 2x - \tan 2x )-2\cot 3x+\cot 2x - \cot 3x=0$
      $\Leftrightarrow 2\cot 4x-2\cot 3x+\cot 2x - \cot 3x=0$
      $\Leftrightarrow 2.\frac{\sin x}{\sin 4x \sin 3x}-\frac{\sin x}{\sin 2x \sin 3x}=0$
      $\Leftrightarrow 2\sin 2x=\sin 4x$
      $\Leftrightarrow \cos 2x=1$
      $\Leftrightarrow x=k \pi     (k \in \mathbb{Z}).$
Như thấy giá trị này không thỏa mãn điều kiện. Vậy PT đã cho vô nghiệm.