|
|
đặt câu hỏi
|
giúp
|
|
|
|
tìm GTLN, GTNN của hàm số theo m:a, y= x&space;+1) trên [-1;3]b, trên [-1;3]b,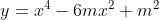 trên [-2;1] trên [-2;1]
|
|
|
|
|
|
đặt câu hỏi
|
tính xác xuất
|
|
|
|
một hộp đựng 5 bi xanh , 6 bi đỏ , 7 bi vàng ( các viên khác nhau ). chọn ngẫu nhiên 8 viên bi . tính xác xuất để 8 viên có đử cả 3 màu
|
|
|
|
đặt câu hỏi
|
tính giới hạn
|
|
|
|
$\mathop {\lim }\limits_{x \to 7}$ $\frac{\sqrt{x+2 } - \sqrt[3]{x+20}}{\sqrt[4]{x+9} -2}$
|
|
|
|
giải đáp
|
giup minh`
|
|
|
|
ta đặt $U_n$=$A_n$ +$x$ => $A_n$ +$x$ = $\frac{5A_{n-1}+5x-1}{A_{n-1}+x+3}$ bạn quy đồng lên ta được $A_n$=$\frac{A_{n-1}(5-x)-x^{2}+2x-1}{A_{n-1}+x+5 }$ (1) từ đây ta chọn $x$ : $-x^{2}+2x-1$=0 => $x$=1 =>$A_1$= 1 => $A_n$= $\frac{4A_{n-1}}{A_{n-1}+6}$ ( bạn thay x=1 vào (1) là ra à ) đến đây thì ở dạng cơ bản rồi chỉ cần nghịch đảo rồi đưa về dùng cấp số cộng hoặc cấp số nhân là được . chúc bạn thành công ( mình rất thích học dạng này bạn có đề thì post cùng làm nếu mình làm được ) |
|
|
|
giải đáp
|
Dãy số 11
|
|
|
|
cái này thì thực sự có rất nhiều cách , ví dụ như tìm mootij vài số hạng đầu rồi dự đoán công thức (phải cm = quy nạp) tìm số hạng tổng quát = giải phương trình đặc trưng , = dùng cấp số công cấp số nhân ,...... mấy cái này bạn nên mua sách tham khảo ý , có hết , nhưng phần này thì các sách viết rất khó hiểu , nên mua của bộ giáo dục thì nó đễ hiểu hơn một chút thui
|
|
|
|
|
|
giải đáp
|
Vui học Toán
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
gap lam
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
giup voi mai hoc roj
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
đặt câu hỏi
|
dãy số 2 ,giúp nha mọi người
|
|
|
|
cho $(u_n)$ \begin{cases}u_1=1 \\ u_{n}= \frac{u_n-1}{\sqrt{3u_{n-1}^{2}+1}} ,n\geq 2 \end{cases} tính lim $(u_n)$ |
|
|
|
đặt câu hỏi
|
dãy số, mọi người giúp với
|
|
|
|
cho dãy $(u_n)$ \begin{cases}u_1=\frac{1}{2} \\ u_{n+1}=\frac{1}{2-u_n} \forall n\geq 1 \end{cases} chứng minh dãy $(u_n)$ có giới hạn , tính giới hạn đó
|
|
|
|
|
|
đặt câu hỏi
|
hình 11 giúp với. thank
|
|
|
|
cho tứ diện $ABCD$ điển $O$ nằm trong tam giác $BCD$ . Từ $O$ kẻ các đường thẳng $//$ với $AB$,$AC$,$AD$. cắt các mặt $(ACD)$,$(ABD)$,$(ABC)$, lần lượt tại $M$,$N$,$P$ a, cm $\frac{OM}{AB}$+$\frac{ON}{AC}$+$\frac{OP}{AD}$ là hằng số b, tìm giá trị lớn nhất của $OM.ON.OP$ các bạn làm giúp mình được câu nào cũng được |
|
|
|
đặt câu hỏi
|
hình 11,giúp với
|
|
|
|
trong mặt $(\alpha)$ cho tam giác $ABC$ vuông tại $A$, $\widehat{ACB} =60$ , $AB=a$ , $O$ là trung điểm của $BC$ , lấy $S \notin (\alpha)$ sao cho $SB=a$ và $SB$ vông góc với $OA$ , , $M $là điểm trên $AB$, $(\beta)$ qua $M // SB,OA$, $(\beta)$ cắt $BC,SC,SA,$ lần lượt là $N,P,Q,$ đặt $BN=x$, chứng minh:$a,$ $MNPQ$ là hình thang vuông, tính theo $a,x$ diện tích hình thang là $b,$ tìm $x$ để diện tích $MNPQmax$ |
|