|
|
bình luận
|
XÁC SUẤT
đúng là 2520 rồi cảm ơn nha
|
|
|
|
|
|
|
|
|
|
giải đáp
|
anh chị giúp em câu này với ạ. em cảm ơn nhiều ạ
|
|
|
|
gọi M(x1;y1) là trung điểm ABgọi G(a;2-a)
ta có \overrightarrow{CG}=2\overrightarrow{GM} TỪ ĐÓ TÌM toạ độ điểm M theo a thay toạ độ M theo a vừa tìm đc vào pt AB =>toạ độ M tham số điểm B(3-2b;b) ta có: 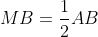 =>toạ độ điểm B =>toạ độ A
|
|
|
|
bình luận
|
XÁC SUẤT
sai rồi bạn ơi! mình ghi đáp án là 2520 mà sai
|
|
|
|
|
|
|
|
giải đáp
|
trước 10h30 nha
|
|
|
|
từ pt AB,AM giải được A(1;4) từ pt AB,BN giải được B(3;5) giao điểm của AM và BN là G nên giải được G(6;-1) áp dụng tc trọng tâm ta tìm được C(14;-12) ĐẾN ĐÂY VIẾT CÁC PT THEO PT CHÍNH TẮC CHO NHANH NHÉ BẠN! CHÚC BẠN THÀNH CÔNG |
|
|
|
đặt câu hỏi
|
BÀI NÀY NỮA
|
|
|
|
1//Cho dãy số $u1=1,u_{n+1}$$=\sqrt{2+u_{n}^{2}}$. Tổng $u_{1}^{2}$+$u_{2}^{2}$$+$...$u_{2016}^{2}$ bằng bao nhiêu? 2//Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một
mặt phẳng. Lấy M, N trên đoạn AC và BF sao cho AM/AC=BN/BF=1/3, Kẻ MM'//AB,NN'//AB$(M'\in AD,N'\in AF)$ . Tỉ số MM'/NN'=? |
|
|
|
đặt câu hỏi
|
XÁC SUẤT
|
|
|
|
Số các số tự nhiên có 5 chữ số khác nhau sao cho hai chữ số ở hai đầu và chữ số
đứng ở vị trí chính giữa đều là số lẻ là ? |
|
|
|
đặt câu hỏi
|
GIÚP MÌNH NHA!
|
|
|
|
I, Cho tứ diện ABCD đều cạnh 4 cm. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi
K là điểm thuộc cạnh BD sao cho KB = 2KD. Chu
vi thiết diện của tứ diện khi cắt bởi (IJK) bằng bao nhiêu?(Tính chính xác đến hai chữ số thập phân) II, Trong không gian cho tam giác ABC, gọi Bx, Cy là hai nửa đường thẳng song song
nằm về cùng một phía đối với (ABC), lấy M, N lần lượt trên Bx, Cy sao cho CN =
2BM. Gọi I là giao điểm của MN với (ABC), E là điểm thuộc AM sao cho EM=1/3 EA,F là giao điểm của IE và AN, Q là
giao điểm của BE và CF. Tỉ số BE/BQ(Nhập kết quả dưới dạng số thập phân thu gọn) |
|
|
|
đặt câu hỏi
|
BÀI NỮA
|
|
|
|
Cho tứ diện ABCD đều cạnh 4
cm. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là điểm thuộc cạnh BD sao
cho KB = 2KD. Diện tích thiết diện của tứ diện khi cắt bởi (IJK) bằng BAO NHIÊU?
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 05/03/2016
|
|
|
|
|
|
|
|
sửa đổi
|
mọi người thử bài này
|
|
|
|
mọi người thử bài này $\mathop {\lim }\limits_{x \to 0} $=\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{x}
mọi người thử bài này $\mathop {\lim }\limits_{x \to 0}=\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{x} $
|
|
|
|
sửa đổi
|
mọi người thử bài này
|
|
|
|
mọi người thử bài này $\mathop {\lim }\limits_{x \to 0}$\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{x l}
mọi người thử bài này $\mathop {\lim }\limits_{x \to 0}$ =\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{x}
|
|
|
|
sửa đổi
|
mọi người thử bài này
|
|
|
|
mọi người thử bài này \mathop {\lim }\limits_{x \to 0} =\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{xl}
mọi người thử bài này $\mathop {\lim }\limits_{x \to 0} $\frac{\sqrt{1+2x}.\sqrt[3]{1+4x}-1}{xl}
|
|