|
|
sửa đổi
|
Phương trình lôgarit
|
|
|
|
Phương trình lôgarit Giải phương trình$\log_{5x+9}(x^2 + 6x + 9) + \log_{x+3}(5x^2 + 24x + 27) = 4$
Phương trình lôgarit a) Giải phương trình$\log_{5x+9}(x^2 + 6x + 9) + \log_{x+3}(5x^2 + 24x + 27) = 4$ b) $\left\{ \begin{array}{l} \sqrt{x-1}+\sqrt{2-y}=1 (1)\\ 3\log_9(9x^2)-\log_3 y^3=3 (2) \end{array} \right.$c) $\log_{2x-1}(2x^2+x-1)+\log_{x+1}(2x-1)^2=4$.d) $\log_2^2(x+1)-6\log_2\sqrt{x+1}+2=0$e) $ \left\{ \begin{array}{l} x + \sqrt{x^2 - 2x + 2} = 3^{y-1} +1\\ y +\sqrt{y^2 - 2y +2} = 3^{x-1} +1\end{array} \right. $f) $\begin{array}{l}1)\,\,\left( {2 + \sqrt {{x^2} - 7x + 12} } \right)\left( {\frac{2}{x} - 1} \right) \le \left( {\sqrt {14x - 2{x^2} - 24} + 2} \right){\log _x}\frac{2}{x}\\\\2)\,\sqrt {{x^2} - 5x + 6} + x + \sqrt {10x - 2{x^2} - 12} + 3{\log _4}\frac{3}{x} \ge 3\end{array}$g) Tìm các giá trị của tham số m để phương trình sau có nghiệm $\log_5(5^x+1).
|
|
|
|
giải đáp
|
các anh đang học logarit ạ. e cũng mún hoj
|
|
|
|
b) Vì $2>1$ nên theo tính chất hàm mũ ta có
$\sqrt{x^2-3x+3}>\sqrt{x}\Leftrightarrow x^2-3x+3>x \Leftrightarrow x^2-4x+3>0\Leftrightarrow (x-1)(x-3)>0$
$\Leftrightarrow x>3$ hoặc $0\le x<1$.
|
|
|
|
giải đáp
|
Hệ phương trình
|
|
|
|
Từ $y^2=6x+y-xy-2x^2$ thay vào PT thứ nhất và tìm $y$ theo $x$
$y=-\frac{x^2-5x-5}{x}$ với $x\ne 0$ ta được PT
$(2x^4-10x^3+15x^2+45x+25)(x-1)=0$
và tìm được
$(x,y)=(1;2)$
$(x,y)=(1;-2)$
|
|
|
|
giải đáp
|
Phương trình trị tuyệt đối.
|
|
|
|
Mình làm thử một trường hợp nhé. Nếu bạn quan tâm chúng ta sẽ trao đổi tiếp.
Xét $x \ge 1$. PT
$x+1+m(x-1)=\left(m+1\right)\left(3x+7\left|mx+5\right|\right)\Leftrightarrow mx+1+x-m=3mx+3x+7(m+1)\left|mx+5\right|$
Nếu $mx+5 \ge 0$ thì PT $\Leftrightarrow mx+1+x-m=3mx+3x+7(m+1)(mx+5)\Leftrightarrow x=-\frac{36m+34}{7m^2+9m+2}$
Nếu $mx+5< 0$ thì PT $\Leftrightarrow mx+1+x-m=3mx+3x-7(m+1)(mx+5)\Leftrightarrow x=-\frac{36+34m}{7m^2+5m-2}$
|
|
|
|
|
|
giải đáp
|
hệ phương trình
|
|
|
|
Đặt $1/y=a$ thì PT đưa về dạng $\begin{cases}f(x)=a^3 \\ a^2+a=g(x) \end{cases}\Rightarrow \sqrt[3]{f^2(x)}+\sqrt[3]{f(x)}=g(x)$ Với $f(x)=x^3+2x^2-5x-4, g(x)=2-x^2+x$ Vaf ta có PT Theo $x$ $2\,{x}^{6}-2\,{x}^{5}-12\,{x}^{4}+11\,{x}^{3}+26\,{x}^{2}-19\,x-20=0$ PT này có nghiệm không đẹp.  |
|
|
|
giải đáp
|
Giải giúp em phương trình
|
|
|
|
Bài này vô nghiệm nhưng có lẽ có một vài sai sót ở đề bài. Mình xin đưa ra phương pháp đồ thị để giải quyết 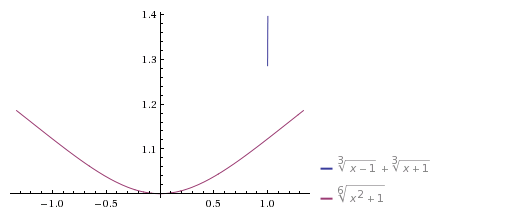 |
|
|
|
giải đáp
|
Hệ phương trình chứa tham số
|
|
|
|
a) Viết lại hệ đã cho dưới dạng
$\begin{cases}(x-1)^2 \le 2-m \\(x+2)^2 \le 3(2-m) \end{cases}$
Để hệ vô nghiệm thì cần $2-m<0\Leftrightarrow m>2$.
Như vậy ngược lại để hệ có nghiệm thì $m \le 2.$
|
|
|
|
giải đáp
|
[Toán 10] Giải và biện luận phương trình
|
|
|
|
b) Điều kiện $x \ge m/4$.
PT $\Leftrightarrow (2m+3x)^2=(4x-m)^2\Leftrightarrow (2m+3x)^2-(4x-m)^2=0\Leftrightarrow (7x+m)(3m-x)=0$
Nếu $7x+m=0\Leftrightarrow x=-m/7$ . Thỏa mãn $\Leftrightarrow m\le 0.$
Nếu $-x+3m=0\Leftrightarrow x=3m$ . Thỏa mãn $\Leftrightarrow m> 0.$
|
|
|
|
giải đáp
|
Bài nữa các ads ơi
|
|
|
|
Bài tập này thuộc dạng ứng dụng tích phân để tìm giới hạn. Mình nghĩ bạn cũng có kiến thức về phần này.
Gợi ý như sau
$\displaystyle\ e^{\displaystyle\lim_{n\to+\infty}\frac{3}{n}\sum_{i=1}^{n}\ln(2+\frac{15i-2}{5n})}=e^{3\int_{0}^{1}\ln(2+3x)dx} $
|
|
|
|
giải đáp
|
giải pt
|
|
|
|
Nếu đề bài của bạn là chính xác thì không có cách biểu diễn sơ cấp nào cho ta nghiệm. Ta chỉ tính được kết quả xấp xỉ  |
|
|
|
|
|
giải đáp
|
Một bài toán giải phương trình
|
|
|
|
Đặt $f(x)=\frac{(x^2-x+1)^3}{x^2(x-1)^2}$
Ta có $f'(x)= \frac{(x^2-x+1)^2(x-2)(x+1)(2x-1)}{x^3(x-1)^3}$
Như vậy $f$ cùng dấu với $(x-2)(x+1)(2x-1)x(x-1)$.
Lập bảng biến thiên của $f$ và từ PT ban đầu $f(x)=f(a)$ ta biện luận.
Ví dụ trên đoạn $(1,2]$ thì $f'<0$ thì $f$ là hàm nghịch biến trên khoảng này và từ
$f(x)=f(a)\Leftrightarrow x=a$ với $a \in (1,2]$.
|
|
|
|
|
|
sửa đổi
|
giúp mình bài nữa với
|
|
|
|
Nhận thấy $\cos x=0$ không là nghiệm của PT nên PT$\Leftrightarrow \sqrt{2-\sin3x}=-\tan x\Leftrightarrow \begin{cases}\tan x \le 0 \\ 2- \sin 3x =\tan^2 x \end{cases}$ Với $2- \sin 3x =\tan^2 x\Leftrightarrow 2+ 4\sin^3x -3\sin x=\frac{1}{1-\sin^2 x}-1$ Đặt $t=\sin x $ ta có $2+ 4t^3 -3t=\frac{1}{1-t^2 }-1$$\Leftrightarrow (2t^2+t-2)(2t^3-t^2-t+1)=0$ Đến đây thì PT bậc 3 không có nghiệm đẹp, còn PT bậc 2 thì đơn giản để tìm nghiệm.
|
|