Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Với điều kiện $n\in R, n\geq  2$, ta có:
       $C^{n-1}_n+C^{n-2}_n=55 \Leftrightarrow n+\frac{n(n-1)}{2}=55 \Leftrightarrow  2n+n^2-n=110  $
                         $\Leftrightarrow  n^2+n-110=0 \Leftrightarrow n=10  $( nhận) hoặc $n=-11$(loại)
Chọn $n=10$
Nhị thức Niu tơn $(\sqrt[7]{8}+\sqrt[3]{5})^n$ có số hạng tổng quát là $C^k_{10}(\sqrt[7]{8})^{10-k}(\sqrt[3]{5})^k  $, với $k=0, 1, 2, ..., 10$
Để số hạng này là số nguyên thì điều kiện cần và đủ là $10-k$ là bội của 7 và k là bội của 3. Điều này chỉ xảy ra với $k=3$
Vậy số hạng là số nguyên là: $C^3_{10}.8.5=4800$

Ta có: $(1+ax)^n=C^0_n+C^1_nax+C^2_na^2x^2+...=1+nax+\frac{n(n-1)}{2}a^2x^2+... $
Theo giả thiết : $\begin{cases}nax=24x \\ \frac{n(n-1)}{2}a^2x^2=252x^2  \end{cases} \Leftrightarrow  \begin{cases}na=24 \\ n(n-1)a^2=504 \end{cases}  $
Từ phương trình đầu ta có: $a=\frac{24}{n} $. Thay vào phương trình sau ta được:
         $n(n-1).\frac{576}{n^2}=504 \Leftrightarrow 72(n-1)=63n \Leftrightarrow 9n=72 \Leftrightarrow n=8    $ (thỏa mãn)
Suy ra $a=3$.
Vậy $n=8, a=3$

Số cách chọn $2$ bác sĩ làm tổ trưởng và tổ phó là một chỉnh hợp chập $2$ của $4$ phần tử.
$\rightarrow   $ Số cách chọn là $A^2_4$
Số cách chọn $5$ y tá làm tổ viên là một tổ hợp chập $5$ của $12$ phần tử.
$\rightarrow  $ Số cách chọn là: $A^5_{12}$
Theo quy tắc nhân, số cách lập đội công tác là: $A^2_4A^5_{12}=9054$

Số số lập được là: $A^5_8=6720$
Phân $6720$ số lập được thành $8$ nhóm theo chữ số hàng đơn vị , mỗi nhóm có $840$ số. Suy ra tổng các chữ số hàng đơn vị là:
              $(1+2+3+4+5+6+7+8).840=30240$
Tường tự tổng các chữ số hàng chục , hàng trăm, hàng nghìn, hàng chục nghìn cũng bằng $30240$
Vậy tổng các số lập được là:
        $(10000+1000+100+10+1).30240=11111.30240=335996640$

Chia cả $2$ vế cho $8^{x}>0$,  Ta có :
PT \( \Leftrightarrow {\left( {\frac{{125}}{8}} \right)^x} + {\left( {\frac{{50}}{8}} \right)^x} = 2 \Leftrightarrow {\left( {\frac{{125}}{8}} \right)^x} + {\left( {\frac{{25}}{4}} \right)^x} - 2 = 0\).
Đặt  \(t = {\left( {\frac{5}{2}} \right)^x} > 0\).  Ta có: 
\({t^3} + {t^2} - 2 = 0\) $\Leftrightarrow (t-1)({t^2}+t+2)=0$ 
                            $\Leftrightarrow t=1$
                            $\Leftrightarrow (\frac{5}{2})^x =1$ 
Đáp số: $x = 0$

$log_2^2x-log_2x^2<0\Leftrightarrow log_2^2x-2log_2x<0 $
$\Leftrightarrow  0<log_2x<2\Leftrightarrow  1<x<4$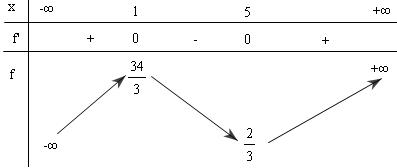

Xét $f(x)=\frac{x^3}{3} -3x^2+5x+9$ thì $f^/(x)=x^2-6x+5$
$\Rightarrow  f(x)>0 \forall x\in(1,4)$ Do đó
Hệ $\begin{cases}log_2^2x-log_2x^2<0 \\ f(x)>0 \end{cases} \Leftrightarrow  1<x<4$