$1.$ Đặt $t = cosx \left( { - 1 \le t \le 1} \right)$
$\begin{array}{l}
PT \Leftrightarrow 2(2{t^2} - 1) - 8t + 7 = \frac{1}{t}\,\,\,(t \ne 0)\\

 \Leftrightarrow \left[ \begin{array}{l}
t = \frac{1}{2}\\
t = 1
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
x =  \pm \frac{\pi }{3} + 2k\pi \\
x = 2k\pi
\end{array} \right.
\end{array}$$,k\in Z$
2. $\frac{b}{{\cos B}} + \frac{c}{{\cos C}} = \frac{a}{{\sin B\sin C}}$

$\Leftrightarrow\frac{2R\sin B}{\cos B}+\frac{2R\sin C}{\cos C}=\frac{2R\sin A}{\sin B\sin C}$

$\begin{array}{l}
 \Leftrightarrow \tan B + \tan C = \frac{{\sin A}}{{\sin B\sin C}} \Leftrightarrow \frac{{\sin (B +
C)}}{{\cos B\cos C}} = \frac{{\sin A}}{{\sin B\sin C}}\\
 \Leftrightarrow \cos B\cos C = \sin B\sin C \Leftrightarrow c{\rm{os}}(B + C) = 0\\
 \Leftrightarrow \cos A = 0 \Leftrightarrow A = \frac{\pi }{2}
\end{array}$
Tam giác $ABC$ vuông tại $A.$

$\cos A.\cos B.\cos C \le \frac{1}{8}$ Thât vậy :
$cosAcosBcosC-\frac{1}{8}=\frac{1}{2}  [cos(A+B)+cos(A-B)]cosC-\frac{1}{8} $
$=\frac{1}{2} [-cos^2C+cos(A-B)cosC-\frac{1}{4} ]$
$=-\frac{1}{2} [(cosC-\frac{1}{2}cos(A-B))^2+\frac{1}{4} -\frac{1}{4}cos^2(A-B) ]$
$=-\frac{1}{2} [(cosC-\frac{1}{2}cos(A-B) )^2+\frac{1}{4} sin^2(A-B)]\leq  0$
Suy ra $cosA.cosB.cosC\leq  \frac{1}{8} $
Dấu $"="$ xảy ra $\Leftrightarrow  \begin{cases}cosC=\frac{1}{2}cos(A-B)  \\ sin(A-B)=0 \end{cases} $
$\Leftrightarrow  A=B=C=\frac{\pi}{3} $ hay $\Delta ABC $ đều

Phương trình $\cos 3x.cos^3x - \sin 3xsin^3x = cos^34x + \frac{1}{4}$ tương đương với :
$cos3x.\frac{cos3x+3cosx}{4}-sin3x.\frac{3sinx-sin3x}{4}=cos^34x+\frac{1}{4}   $
$\Leftrightarrow  \frac{1}{4} coss^23x+\frac{3}{4} cos3xcosx-\frac{3}{4}sin3xsinx+\frac{1}{4}  sin^23x=cos^34x+\frac{1}{4} $
$\Leftrightarrow  \frac{1}{4} +\frac{3}{4} cos4x=coss^34x+\frac{1}{4} \Leftrightarrow  \frac{3}{4} cos4x=cos^34x$

$\Leftrightarrow 4\cos^34x-3\cos 4x=0\Leftrightarrow\cos 12x=0$

$\Leftrightarrow x=\frac{\pi}{24}+\frac{k\pi}{12}, k\in Z$

Gọi $(x;y)$ thì $\overrightarrow{BA}=(1;3)$ và $\overrightarrow{BC}=(x-1;y-1)$
Điều kiện tam giác $ABC$ vuông cân tại $B$
$\left\{ \begin{array}{l} \overrightarrow{BA}.\overrightarrow{BC}\\BA=BC \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} 1.(x-1)+3.(y-1)=0\\ 1^2+3^2=(x-1)^2+(y-1)^2 \end{array} \right. $
$ \Leftrightarrow  \left\{ \begin{array}{l} x=4-3y\\ (3-3y)^2+(y-1)^2=10 \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} x=4-3y\\ 10y^2-20y=0 \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} y=0\\ x=4 \end{array} \right. $ hay $\left\{ \begin{array}{l} y=2\\ x=-2 \end{array} \right. $
Vậy có hai điểm $C$ có tọa độ $(4;0),(-2;2)$.

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

$\begin{array}{l}
\,\,\frac{{{a^2} - {b^2}}}{{{c^2}}} = \frac{{\sin^ 2A - \sin^ 2B}}{{\sin^ 2C}} = \frac{{(1 - \cos 2A) -
(1 - \cos 2B)}}{{2{{\sin }^2}C}}\\
 = \frac{{\cos 2B - \cos 2A}}{{2{{\sin }^2}C}} = \frac{{\sin (A + B)\sin ( A-B)}}{{{{\sin }^2}C}}\\
 = \frac{{\sin C\sin (A - B)}}{{{{\sin }^2}C}} = \frac{{\sin (A - B)}}{{\sin C}}\,\,(dpcm)
\end{array}$

$a)$ Parabol ${y^2} = 4x$ có tiêu điểm $F(1;0)$ và đường chuẩn $x =-1$
Xét điểm $N(-1;a)$ thuộc đường chuẩn. Đường thẳng này tiếp xúc với đường thẳng $kx – y + k + a = 0$
$4{( - 1)^2} = 4k(k + a)$
$ \Leftrightarrow {k^2} + ak - 1 = 0 (1)$
Ta thấy $\forall a$, ($1$) luôn có nghiệm phân biệt có tích ${k_1}{k_2} =- 1$. Do đó $\forall N( -1;a)$thuộc đường chuẩn, từ $N$ luôn kẻ được tới Parabol $2$ tiếp tuyến vuông góc nhau.
$b)$ Tiếp tuyến $N{T_1}$ có tiếp điểm $T1(x_1;y_1)$ và hệ số góc $k_1$, trong đó $y_1$ là nghiệm kép của $(3)$ ứng với $k = k1 \Rightarrow {y_1} = \frac{2}{{{k_1}}} \Rightarrow {x_1} = \frac{1}{4}\,;y_1^2 = \frac{1}{{k_1^2}}$
Tương tự tiếp tuyến $NT_2$ có tiếp điểm $T2(x_2;y_2)$ với ${x_2} = \frac{1}{{k_2^2}};{y_2} = \frac{2}{{{k_2}}}$. Xét các véc tơ $\overrightarrow {F{T_1}} ;\overrightarrow {F{T_2}} $
$\begin{array}{l}
\overrightarrow {F{T_1}}  = \left( {{x_1} - 1;{y_1} - 0} \right) = \left( {\frac{1}{{k_1^2}} -
1;\frac{1}{{{k_1}}}} \right) = \left( {\frac{{1 - k_1^2}}{{k_1^2}};\frac{2}{{{k_1}}}} \right)\\= \frac{1}{{{k_1}}}(a;2)
\end{array}$
Do $k_1; k_2$ là nghiệm của ($4$) $ \Rightarrow 1 - k_1^2 = a{k_1}$
Tương tự:
$\overrightarrow {F{T_1}}  = \frac{1}{{{k_2}}}(a;2)$
Do đó $\overrightarrow {F{T_1}} ;\overrightarrow {F{T_2}} $ là 2 véc tơ cộng tuyến $ \Rightarrow
F;{T_1};{T_2}$ thẳng hàng  $\Leftrightarrow  {T_1}{T_2}$ luôn đi qua điểm đố định $F(1;0).$
$c)$ Giả sử $M(x_0;y_0)$ thuộc Parabol, $M \ne 0$ tức là $y_0^2 = 4x,{x_0} \ne 0$. Tiếp tuyến tại $M$ có phương trình:
${y_0}y = 2({x_0} + x)\,\,\,(5)$
Cho $x = 0$, $(5) \Rightarrow y = \frac{{2{x_0}}}{{{y_0}}} = \frac{{4{x_0}}}{{2{y_0}}} = \frac{{{y_0}}}{2}$ là tung độ của $B$
Cho $y = 0 (5) \Rightarrow x =  - {x_0} =  - \frac{{y_0^2}}{4}$ là hoành độ của $A$.
Trung điểm $I$ của $AB$ có tọa độ :
$\begin{array}{l}
\left\{ \begin{array}{l}
{x_I} = \frac{{{x_A}}}{2} =  - \frac{{y_0^2}}{8}\\
{y_I} = \frac{{{y_B}}}{2} = \frac{{{y_0}}}{4}
\end{array} \right. \Rightarrow {y_0} = 4{y_I}\\
 \Rightarrow {x_I} =  - \frac{{{{(4{y_I})}^2}}}{8} = -2y_I^2 \Leftrightarrow y_I^2 =  - \frac{1}{2}{x_I}
\end{array}$
Quỹ tích $I$ là parabol với phương trình ${y^2} = - \frac{1}{2}x$

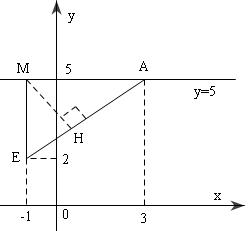 Phương trình ($C$): ${\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9 \Rightarrow E( - 1;2),\,R = 3$
Dễ thấy đường thẳng $x = 3$ qua $A(3;5)$ và không tiếp xúc với ($C$). Do đó chỉ cần xét các đường thẳng qua $A$ và không song song với $Oy$, đường thẳng qua $A$, hệ số góc $k$ có phương trình $y = k(x-3) + 5 $
$ \Leftrightarrow kx - y - 3k + 5 = 0$
Đường thẳng này là tiếp tuyến của ($C)\Leftrightarrow    $khoảng cách từ $E$ đến đường thẳng $= R.$
$ \Leftrightarrow \frac{{| - k - 2 - 3k + 5|}}{{\sqrt {{k^2} + 1} }} = 3 \Leftrightarrow (3-4k)^2=9(k^2+1)\Leftrightarrow \left[
\begin{array}{l}
k = 0\\
k = \frac{{24}}{7}
\end{array} \right.$
Vậy qua A kẻ được tới đường tròn $2$ tiếp tuyến, phương trình của chúng là:
$y = 5;y = \frac{{24}}{7}(x - 3) + 5 = \frac{{24}}{7}x - \frac{{37}}{7}$
Gọi $M$ là tiếp điểm của đường thẳng $y = 5$ với ($C$) thì $\Delta AME$ vuông ở $M$ và có $EM = 3, AM = 4$
$\begin{array}{l}
 \Rightarrow AE = 5\\
 \Rightarrow MH = \frac{{EM.AM}}{{AE}} = \frac{{12}}{5}
\end{array}$
($MH$ là đường cao $\Delta AME$ $ \Rightarrow MH = \frac{1}{2}MN)$
$ \Rightarrow MN = 2MH = \frac{{24}}{5}$

Có $\sin A(1 - \sin B) + \sin B(1 - \sin C) + \sin C(1 - \sin A) > 0$
$ \Rightarrow \sin A + \sin B + \sin C - \sin A\sin B - \sin B\sin C - \sin C\sin A > 0$
Và có $(1 - \sin A)(1 - \sin B)(1 - \sin C) > 0$
$ \Rightarrow \sin A + \sin B + \sin C - \sin A\sin B - \sin B\sin C - \sin C\sin A$
$ < 1 - \sin A\sin
B\sin C < 1$
$ \Rightarrow \sin A + \sin B + \sin C - \sin A\sin B - \sin B\sin C - \sin C\sin A < 1$ (đpcm)

$\begin{array}{l}
1.  \,\frac{{\sqrt 3 }}{{c{\rm{o}}{{\rm{s}}^2}x}} < 4\tan x \Leftrightarrow \sqrt 3 ({\tan ^2}x + 1) < 4\tan x\\
 \Leftrightarrow \frac{1}{{\sqrt 3 }} < {\mathop{\rm t}\nolimits} {\rm{anx}} < \sqrt 3 \\
 \Leftrightarrow \frac{\pi }{6} + k\pi  < x < \frac{\pi }{3} + k\pi ,k \in Z
\end{array}$
$\left. \begin{array}{l}
2.  \,\,{b^2} + {c^2} = 2m_a^2 + \frac{{{a^2}}}{2}\\
\,{a^2} + {c^2} = 2m_b^2 + \frac{{{b^2}}}{2}\\
\,{b^2} + {a^2} = 2m_c^2 + \frac{{{c^2}}}{2}
\end{array} \right\} \Rightarrow {a^2} + \,{b^2} + {c^2} = \frac{4}{3}({3^2} + {4^2} + {5^2})
= \frac{{200}}{3}$
$ \Rightarrow \,{a^2} + 2m_a^2 + \frac{{{a^2}}}{2} = \frac{{200}}{3} \Rightarrow a =
\frac{{10}}{3}cm$
Tương tự: $b = \frac{{4\sqrt {13} }}{3}\,\, ;\,\,c = \frac{{2\sqrt {73} }}{3}$
Theo định lý hàm số cosin:
$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \sqrt {\frac{{625}}{{949}}}  \Rightarrow \cos
A > \frac{1}{{\sqrt 2 }} \Rightarrow A < {45^0}$

Điều kiện có nghĩa: $x \ne 1$. Biến đổi tương đương bất phương trình:
$\begin{array}{l}
\sqrt {{a^3}}{{(x - 1)}^2}  + \frac{{\sqrt a }}{{{{\left( {x - 1} \right)}^2}}} \le

\sqrt[4]{{{a^3}}}\left| {\sin \frac{{\pi x}}{2}} \right|\\
 \Leftrightarrow \sqrt {{a^3}} {\left( {x - 1} \right)^4} - \sqrt[4]{{{a^3}}}\left| {\sin \frac{{\pi

x}}{2}} \right|{(x - 1)^2} + \sqrt a  \le 0\\
 \Leftrightarrow \left( {\sqrt[4]{{{a^3}}}{{(x - 1)}^2} - \frac{1}{2}\left| {\sin \frac{{\pi x}}{2}}

\right|} \right)^2 + \sqrt a  - \frac{1}{4}{\sin ^2}\frac{{\pi x}}{2} \le 0
\end{array}$
Nếu $a > \frac{1}{16} $ thì $\sqrt a  - \frac{1}{4}{\sin ^2}\frac{{\pi x}}{2}> 0$ với mọi $x$ nên bất pt vô nghiệm.
Nếu $a = \frac{1}{16} $ thì bpt trở thành:
$\begin{array}{l}
{\left( {\frac{1}{8}{{(x - 1)}^2} - \frac{1}{2}\left| {\sin \frac{{\pi x}}{2}} \right|} \right)^2} +
\frac{1}{4}\left( {1 - {{\sin }^2}\frac{{\pi x}}{2}} \right) \le 0\\
 \Leftrightarrow \left\{ \begin{array}{l}
{\sin ^2}\frac{{\pi x}}{2} = 1\\
\frac{1}{8}{(x - 1)^2} = \frac{1}{2}\left| {\sin \frac{{\pi x}}{2}} \right|
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 3\\
x =  - 1
\end{array} \right.
\end{array}$
Vậy $a =\frac{1}{16} $ là giá trị lớn nhất để bất pt có nghiệm.

Vì ${\mathop{\rm t}\nolimits} {\rm{anx}} + \cot 2x = \frac{{\sin {\rm{x}}\sin 2x + \cos x\cos
2x}}{{\cos x\sin 2x}} = \frac{{\cos x}}{{\cos x\sin 2x}}$$ = \frac{1}{{\sin 2x}}$
$
\Rightarrow f(x) = \sin 3x\sin 4x\sin 2x = \frac{1}{2}\left( {\cos x - c{\rm{os}}7x} \right)\sin 2x  $$
                  = \frac{1}{2}\sin 2x\cos x - \frac{1}{2}\sin 2x\cos 7x\\ $
$= \frac{1}{4}\left( {{\mathop{\rm s}\nolimits} {\rm{inx}} + \sin 3x} \right) - \frac{1}{4}\left( {\sin
( - 5x) + \sin 9x} \right) $
$= \frac{1}{4}{\mathop{\rm s}\nolimits} {\rm{inx}} +
\frac{1}{4}{\mathop{\rm s}\nolimits} {\rm{in3x + }}\frac{1}{4}{\mathop{\rm s}\nolimits}
{\rm{in5x - }}\frac{1}{4}{\mathop{\rm s}\nolimits} {\rm{in9x}}\\
\Rightarrow \int {f(x)dx}  =  - \frac{1}{4}\cos x - \frac{1}{{12}}c{\rm{os}}3x -
\frac{1}{{20}}c{\rm{os}}5x + \frac{1}{{36}}c{\rm{os}}9x + C
$

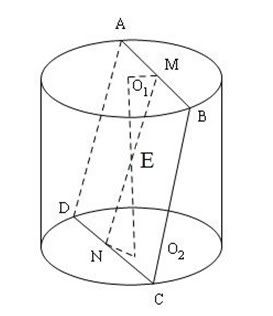Kí hiệu $O_1; O_2$ là tâm $2$ đáy. $M$ và $N$ là trung điểm các dây $AB, CD$. Ta có $MN \bot AB$ và $MN  \bot CD.$
$\widehat {{O_1}MN} = \widehat {MN{O_2}} = {45^0}=$ góc giữa ($ABCD$) và $2$ mặt đáy hình trụ
 $\begin{array}{l}
 \Rightarrow N{O_2} = {O_2}E = {O_1}E = ME.\frac{{\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}\\
 \Rightarrow {O_1}{O_2} = \frac{{a\sqrt 2 }}{2}
\end{array}$
$\begin{array}{l}
{O_2}{C^2} = {O_2}{N^2} + N{C^2} = {\left( {\frac{{a\sqrt 2 }}{4}} \right)^2} + {\left(
{\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{8}\\
 \Rightarrow {O_2}C = \frac{{a\sqrt 6 }}{4}\\
 \Rightarrow {S_{xq}} = 2\pi .{O_2}C.{\rm{O}}{{\rm{O}}_1} = \frac{{{a^2}\sqrt {3\pi } }}{2}\\
V = \pi.O_2C^2.O_1O_2=\frac{{3\sqrt 2 \pi {a^3}}}{{16}}
\end{array}$

Đường tròn đã cho có tâm $E(1;-3)$ bán kính $R = 5$. Giả sử ($d$) là đường thẳng qua gốc $O$ và cắt
đường tròn thành một dây cung $AB$ có độ dài bằng $8$. Gọi $F$ là trung điểm của $AB$ thì $FB = 4$,
${\rm{EF}} \bot FB$
$ \Rightarrow {\rm{E}}{{\rm{F}}^2} = {R^2} - {4^2} \Rightarrow {\rm{EF}} = 3$
Vậy ($d$) là đường thẳng qua gốc $O$ và cách $E(1;-3)$ một khoảng bằng $3$. Nếu $d  \bot Ox$, thì ($d$) cách $E$ một khoảng bằng $1$ (loại)
Nếu ($d$) không vuông góc $Ox$ thì gọi $a$ là hệ số góc của ($d)  \Rightarrow (d)$ có phương trình: $ax – y = 0$ $ \Rightarrow E(1; - 3)$cách $d$ một khoảng $h = \frac{{|a + 3|}}{{\sqrt {{a^2} + 1} }}$
Do đó phải có $h = 3 \Leftrightarrow   (a+3)^2=9(a^2+1)\Leftrightarrow a = 0$ hoặc $a = \frac{3}{4} $
Đáp số: $y = 0$ hoặc $y = \frac{3}{4}x$