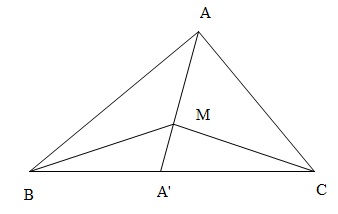
Gọi $A’$ là giao điểm của $MA$ với $BC$.
Ta có : $\overrightarrow {MA'} = \frac{{A'C}}{{BC}}\overrightarrow {MB} + \frac{{A'B}}{{BC}}\overrightarrow {MC} $
Và
$\frac{{A'C}}{{A'B}} = \frac{{S\left( {MA'C} \right)}}{{S\left( {MA'B}
\right)}} = \frac{{S\left( {MAC} \right)}}{{S\left( {MAB} \right)}} =
\frac{{{S_b}}}{{{S_c}}}$
\(\begin{array}{l}
\Rightarrow \left\{ \begin{array}{l}
\frac{{A'C}}{{BC}} = \frac{{{S_b}}}{{{S_b} + {S_c}}}\\
\frac{{A'B}}{{BC}} = \frac{{{S_c}}}{{{S_b} + {S_c}}}
\end{array} \right.
\Rightarrow
\overrightarrow {MA'} = \frac{{{S_b}}}{{{S_b} + {S_c}}}\overrightarrow
{MB} + \frac{{{S_c}}}{{{S_b} + {S_c}}}\overrightarrow {MC} (*)
\end{array}\)
Mặt
khác $\frac{{MA'}}{{MA}} = \frac{{S\left( {MA'B} \right)}}{{S\left(
{MAB} \right)}} = \frac{{S\left( {MA'C} \right)}}{{S\left( {MAC}
\right)}} = \frac{{S\left( {MA'B} \right) + S\left( {MA'C}
\right)}}{{S\left( {MAB} \right) + S\left( {MAC} \right)}}$
$\,\, = \frac{{{S_a}}}{{{S_b} + {S_c}}}$
$ \Rightarrow \overrightarrow {MA'} = \frac{{ - {S_a}}}{{{S_b} + {S_c}}}\overrightarrow {MA} $. Thay vào (*) được
$-$${S_a}\overrightarrow
{MA} = {S_b}\overrightarrow {MB} + {S_c}\overrightarrow {MC}
\Rightarrow {S_a}\overrightarrow {MA} + {S_B}\overrightarrow {MB} +
{S_c}\overrightarrow {MC} = \overrightarrow 0 $ (đpcm)
Chú ý:
Đây là một tính chất quen thuộc. Khi $M$ nằm ngoài tam giác, ta cũng có
đẳng thức tương tự, nhưng đổi dấu một số hạng tử vế trái tương ứng.