|
|
Ta sẽ chứng minh bài toán trong trường hợp $\Delta ABC$ nhọn. Các trường hợp khác chứng minh hoàn toàn tương tự.
Bổ đề: Với điểm $M$ nằm trong $\Delta ABC$ ta kí hiệu $S_a=S_{MBC},S_b=S_{MCA},S_c=S_{MAB}$. Khi đó:
\[ S_a.\overrightarrow{MA}+S_b.\overrightarrow{MB}+S_c.\overrightarrow{MC}=\overrightarrow{0}\].
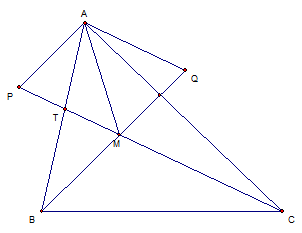
Chứng minh:
Vì $M$ nằm trong $\Delta ABC$ nên $S_a,S_b,S_c>0$.
Qua $A$ dựng các đường thẳng song song với $BM$ và $CM$, cắt $CM$ và $BM$ tương ứng tại $P$ và $Q$.
Ta có: $\frac{S_b}{S_a}\overrightarrow{MB}=\frac{S_{MCA}}{S_{MBC}} \overrightarrow{MB}=\frac{AT}{BT}\overrightarrow{MB}=\frac{AP}{BM}\overrightarrow{MB}=\overrightarrow{AP}$.
Tương tự: $\frac{S_c}{S_a}\overrightarrow{MC}=\overrightarrow{AQ}$.
Từ đó suy ra đpcm.
Trở lại bài toán:
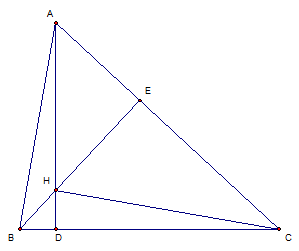
Kí hiệu $S=S_{ABC}$. Từ bổ đề trên ta có: $\frac{S_a}{S}\overrightarrow{HA}+\frac{S_b}{S}\overrightarrow{HB}+\frac{S_c}{S}\overrightarrow{HC}=\overrightarrow{0}$.
Ta có: $\frac{S_a}{S}=\frac{HD}{BD}.\frac{BD}{AD}=\cot \widehat{BHD}.\cot \widehat{ABD}=\cot C.\cot B=\frac{1}{\tan B\tan C} $.
Tương tự: $\frac{S_b}{S}=\frac{1}{\tan C\tan A},\frac{S_c}{S}=\frac{1}{\tan A\tan B}$.
Từ đó suy ra đpcm.
|