câu hỏi toán học

Question

cho lăng trụ đứng ABC.A'B'C', có đáy ABC là tam giác vuông tại B, AB=a , AA'= 2a , A'C = 3a . gọi M là trung điểm của A'C' I là giao điểm của AM và A'C . tính thể tích IAA'B

score 4 · Answer 1

Bình chọn tăng 4 Bình chọn giảm

Hạ $IH\perp AC (H\in AC)\Rightarrow IH\perp(ABC)$ hay $IH$ là đường cao của tứ diện $IABC$.
Ta có:
$\frac{A'I}{IC}=\frac{A'M}{AC}=\frac{1}{2}\Rightarrow \frac{CI}{CA'}=\frac{2}{3};\frac{A'I}{A'C}=\frac{1}{3}$
$IH//AA'\Rightarrow \frac{IH}{AA'}=\frac{CI}{CA'}=\frac{2}{3}\Rightarrow IH=\frac{2}{3}AA'=\frac{4a}{3}$
Lại có:
$AC=\sqrt{A'C^2-A'A^2}=a\sqrt5;BC=\sqrt{AC^2-AB^2}=2a$
Suy ra:
$S(ABC)=\frac{1}{2}AB.BC=a^2$
$V(IABC)=\frac{1}{3}IH.S(ABC)=\frac{4a^3}{9}$
$V(A'ABC)=\frac{1}{3}AA'.S(ABC)=\frac{2a^3}{3}$
$V(IAA'B)=V(A'ABC)-V(IABC)=\frac{2a^3}{9}$

score 3 · Answer 2

Xét $\Delta$A'AC vuông tại A => $AC^{2}= (3a)^{2}- (2a)^{2}= 5a^{2}$
Xét $\Delta$ABC vuông tại B => $BC^{2}= 5a^{2}- a^{2}= 4a^{2}$ => BC= 2a
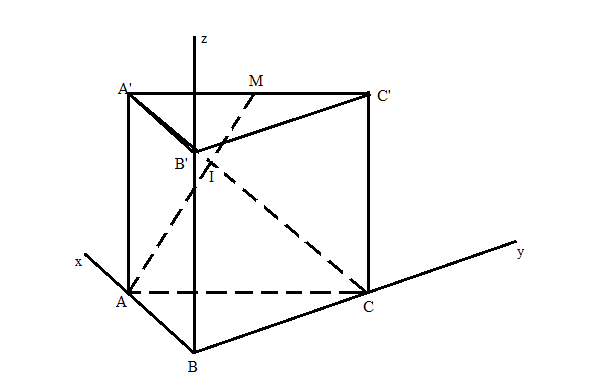
Gắn hệ trục tọa độ vào hình vẽ sao cho B trùng gốc tọa độ, BA trùng Ox, BC trùng Oy, BB' trùng Oz
Khi đó tọa độ các điểm là: B(0,0,0), A'(a, 0, 2a), C(0, 2a, 0), A(a, 0,0), M(a/2, a, 2a)
=> $\overrightarrow{AM}$ (-a/2, a, 2a)= (-1,2,4) => Phương trình AM $\begin{cases}x= a-t_{1} \\ y=2t_{1}\\z=4t_{1} \end{cases}$
$\overrightarrow{A'C}$ (-a, 2a, -2a)= (1,-2,2) => Phương trình A'C $\begin{cases}x= t_{2} \\ y= 2a-2t_{2}\\z=2t_{2} \end{cases}$
Có: I= AM$\cap $A'C => Tọa độ I thỏa mãn : $\begin{cases}a-t_{1}= t_{2} \\ 2t_{1}=2a-2t_{2}\\4t_{1}=2t_{2} \end{cases}$ => $\begin{cases} t_{1}= a/3\\ t_{2}= 2a/3 \end{cases}$
=> I(2a/3, 2a/3, 4a/3)
Lại có phương trình mp(A'AB) là: y=0
=> d(I, (A'AB)) = $\frac{\left| {2a/3} \right|}{\sqrt{1}}$= 2a/3
Mà: $S_{A'AB}$ = 1/2. AA'. AB= $a^{2}$
=> $V_{IAA'B}$= 1/3. d(I, (A'AB)) . $S_{A'AB}$ = $\frac{2a^{2}}{9}$

Đề bài bạn đưa ra đã có những lời giải rất tốt vì trình bày được theo nhiều cách khác nhau, đây là giải theo phương pháp tọa độ lớp 12, lời giải của bạn Khang là theo cách tính trực tiếp lớp 11.