Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Ah ha! Mình có cách đơn giản hơn nhé
Kí hiệu $\sum_{cyc}\frac{x}{x^2+2}=\frac{x}{x^2+2}+\frac{y}{y^2+2}+\frac{z}{z^2+2}$
$cyc$ nghĩa là xoay vòng.
Dễ thấy $\sum_{cyc}\frac{x}{x^2+2} \le \sum_{cyc}\frac{x}{2x+1}=\frac{3}{2}-\frac{1}{2}\sum_{cyc}\frac{1}{2x+1}$
Việc còn lại là chứng minh
$\sum_{cyc}\frac{1}{2x+1} \ge 1$
Do $xyz=1$ nên tồn tại $a, b, c$ sao cho $x=\frac{a}{b}, y=\frac{b}{c}, z=\frac{c}{a}$, như vậy
$\sum_{cyc}\frac{1}{2x+1}=\sum_{cyc}\frac{b}{2a+b}=\sum_{cyc}\frac{b^2}{2ab+b^2} \ge \frac{(a+b+c)^2}{\sum a^2+2\sum ab}=1$

Mình chưa nghĩ ra cách nào ngắn hơn, bạn tham khảo nhé
Đặt $x+y+z=u$ và $xy+yz+zx=v$. BĐT đã cho tương đương với
\[ 4u^2+2v^2-8u-9v-2uv+15 \geq 0 \]
theo BĐT Cô-si, $u^2 \geq 3v \geq 9$. Ta xét $3$ trường hợp
$\text {Trường hợp 1:} \quad v \geq 6$
Ta có $\text{VT}=(u-v)^2+(u-3)(3u+1)+(v-3)(v-6) \geq 0$ và chúng ta xong.
$\text{Trường hợp 2:} \quad 4,5 \leq v \leq 6$
Ta có $\text{LHS}=f(u) \geq f(3)$ vì $f'(u)=8u-2v-8 \geq 8\cdot 3 - 2 \cdot 6 -8 > 0$ và $f(3)=(v-3)(2v-9) \geq 0$ theo giả thiết.
$\text{Trường hợp 3:} \quad 3 \leq v \leq 4,5$
Ta có $\text{LHS}=(u-v)^2+3u^2+v^2-8u-9v+15 \geq 3u^2+v^2-8u-9v+15$
Đặt $g(v)=3u^2+v^2-8u-9v+15$. suy ra $g'(v)=2v-9 \leq 0$ nên $g(v) \geq g\left(\frac{u^2}{3}\right)$
$g\left(\frac{u^2}{3}\right) = \frac{1}{9}(u-3)(u^3+3u^2+9u-45) \geq 0$ vì $u \geq 3$.

Tóm lại ta có ĐPCM.

Sử dụng công thức $\cos 2x=2\cos^2x-1,\cos 2y=1-2\sin^2y$, sau đó nhân hai vế của PT hai với $2i$ và cộng với PT thứ nhất  tiếp đến chia cho $2$ và ta có

$(\cos x+i\sin y)^2+{1\over\cos x+i\sin y}={\sqrt{3}+1+i(\sqrt{3}-1)\over 2}$

Đặt $z=\cos x+i\sin y$. Ta có $z^2+{1\over z}={\sqrt{3}+1+i(\sqrt{3}-1)\over 2}$, Pt này có một nghiệm đẹp $z_1={\sqrt{3}+i\over 2}$. Sau phân tích đa thức thành nhân tử, ta thu được nghiệm thứ hai từ PT bậc hai( kí hiệu là $z_2$) thỏa mãn $|\Re(z_2)|\leqslant 1,|\Im(z_2)|\leqslant 1$, và nó thỏa mãn với điều kiện $z=\cos x+i\sin y$. Nhưng nó  "xấu xí".
Với trường hợp $z_1$, $\cos x+i\sin y={\sqrt{3}+i\over 2}\iff x=\pm{\pi\over 6}+2k\pi\land y=(-1)^m{\pi\over 6}+m\pi$,$k,m\in\mathbb{Z}$

Trừ theo từng vế của hai PT ta được
$-8a-12c=-152\Rightarrow c=-\frac{2}{3}(a-19)$.
Thay vào PT thứ nhất ta được
$a^2+b^2+(-\frac{2}{3}(a-19))^2-12a-6b-14(-\frac{2}{3}(a-19))=-77 $
$\Leftrightarrow b^2-6b+\frac{13a^2}{9}-\frac{176a}{9}+\frac{541}{9}=0$
Với điều kiện $-13a^2+176a-460 \ge0$ thì ta có $b= 3 \pm \frac{1}{3}\sqrt{-13a^2+176a-460}$
Tóm lại $b= 3 \pm \frac{1}{3}\sqrt{-13a^2+176a-460}, c=-\frac{2}{3}(a-19), a \in \mathbb{R} ,-13a^2+176a-460 \ge0$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Ta có:
$y'=\cos ax - ax \sin ax$
$y''=-2a\sin ax-a^2x\cos ax$ 
$y^{(3)}=-3a^2\cos ax+a^3x\sin ax$ 
$y^{(4)}=4a^3\sin ax +a^4x\cos ax$  
Bằng quy nạp, suy ra:  $y^{(n)}=na^{n-1}\cos\left (ax+\frac{(n-1)\pi}{2} \right )+a^nx\cos\left (ax+\frac{n\pi}{2} \right ),\forall n\in\mathbb{N}^*$ .
 Các bạn có thể tham khảo chi tiết của phương pháp này tại đây
 http://toan.hoctainha.vn/Thu-Vien/Chuyen-De/113568/dao-ham-cap-cao

1) Giả sử đã dựng được các điểm $M, N, P$ thỏa mãn yêu cầu bài toán. Gọi $M_1, M_2$ lần lượt là điểm đối xứng của $M$ qua các đường thẳng $AB, AC$. Khi đó
$MP+MN+PN=PM_1+ NM_2+PN \ge M_1M_2$
(đường thẳng thì luôn ngắn hơn đường gấp khúc).
Mặt khác $\triangle AM_1M_2$ cân tại $A$ có $\widehat{M_1AM_2}=2\widehat{BAC}$ không đổi. Như vậy trong các tam giác cân có góc ở đỉnh không đổi, cạnh đáy nhỏ nhất khi cạnh bên nhỏ nhất. Lúc đó ta cần có $AM_1=AM$ nhỏ nhất, tức là $AM$ là đường cao của $\triangle ABC$.
Tương tự thì ta có $M,N,P$ là chân các đường cao kẻ từ $A,B,C$ của $\triangle ABC$.

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Giải phương trình :
\[ 4^{2x+\sqrt{x+2}}+2^{x^3}=4^{2+\sqrt{x+2}}+2^{x^3+4x-4}\]

Ta biết rằng thể tích hình cầu có bán kính $R$ tính bằng công thức $\frac{4}{3}\pi R^3$.
Như vậy giả sử xếp được $13$ có bán kính $r$ thì phần thể tích mà nó chiếm là $\frac{52}{3}\pi r^3$. Mặt khác thì hình hộp này có thể tích $(2r)^2.3,5r=14r^3 < \frac{52}{3}\pi r^3$.
Vậy câu trả lời của bài toán là không.

Bài tập này của bạn khá hay. Tôi xin nêu ra một cách để giải quyết như sau
Trước hết ta nêu ra bổ đề : Trong tất cả những tam giác nội tiếp trong một đường tròn và chung một cạnh đáy, thì tam giác cân là tam giác có diện tích lớn nhất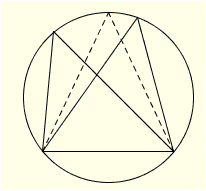

Phần chứng minh của bổ đề này là hiển nhiên vì thấy đỉnh của tam giác cân là đỉnh xa đáy nhất.
Từ đó, bài toán ban đầu có thể trở thành tìm giá trị nhỏ nhất của một tam giác cân nội tiếp đường tròn cho trước.
Giả sử ta có hình vẽ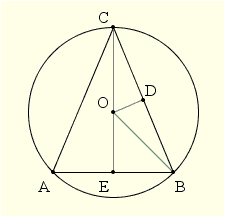

Gọi $\alpha$ là góc ở đ của tam giác cân $ABC\rightarrow \widehat{ACE}= \widehat{BCE}=90^\circ - \alpha$.
Gọi $O$ là tâm của đường tròn bán kính $R$ và $D, E$ là trung điểm của $AB, BC$.
Ta có $ \widehat{BOE}= \widehat{ACB}= 180^\circ-2\alpha\Rightarrow OE=OB. \cos \widehat{BOE}=-R \cos 2\alpha$
Do đó $CE=R(1- \cos 2\alpha)$ và $AB=2EB=2R \sin  2\alpha$.
Từ đó $S_{ABC}=\frac{1}{2}AB.CE=R^2(1- \cos 2\alpha)\sin  2\alpha=4R^2\sin \alpha\cos^3 \alpha.             (1)$
Mặt khác áp dụng BĐT Cô-si ta có
$\sin^2 \alpha\cos^6 \alpha=\frac{1}{3}.3\sin^2 \alpha.\cos^2 \alpha.\cos^2 \alpha.\cos^2 \alpha \le \frac{1}{3}\left ( \frac{3\sin^2 \alpha+\cos^2 \alpha+\cos^2 \alpha+\cos^2 \alpha}{4}\right )^4=\frac{3^3}{4^4}         (2)$
Từ $(1)$ và $(2)$ ta có $S \le \frac{3 \sqrt 3}{4}R^2$.
Như vậy $\max S = \frac{3 \sqrt 3}{4}R^2\Leftrightarrow \triangle ABC$ đều.

Bài tập này là bài tập số $26$, trang $9$, sách Bài tập hình học nâng cao $12$. Bạn có thể đọc và tham khảo tại tài liệu quen thuộc này nhé.