|
|
giải đáp
|
Minh dang can gap giup voi ne
|
|
|
|
1. Gợi ý: Chứng minh bằng quy nạp các đẳng thức sau $A=1+2+\dots+n=\frac1{2}n(n+1)$ $B=1^5+2^5+\dots+n^5=\frac1{12}n^2(n+1)^2(2n^2+2n-1)=A.\frac{n(n+1)(2n^2+2n-1)}{6} $ Dễ thấy $A \in \mathbb N$ nên để chứng minh $A \mid B$ thì chỉ cần chứng minh $\frac{n(n+1)(2n^2+2n-1)}{6} \in \mathbb N$. Tức là phải chứng minh $2 \mid n(n+1)(2n^2+2n-1)$, điều này đơn giản vì $n(n+1)$ là tích của 2 số tự nhiên liên tiếp nên tích này chẵn; và $3 \mid n(n+1)(2n^2+2n-1)$, điều này không khó để chứng minh vì chỉ cần xét $n \in \{ 3k,3k+1,3k+2\}$.
|
|
|
|
giải đáp
|
không có hướng giải luôn..khác câu trước
|
|
|
|
Đặt $t = \sqrt {{e^x} - 1} \Rightarrow {t^2} = {e^x} - 1 \Rightarrow
2tdt = {e^x}dx \Rightarrow dx = \frac{{2tdt}}{{{e^x}}} =
\frac{{2tdt}}{{{t^2} + 1}} $
$\Rightarrow I = \int\limits_0^1
{\frac{{2{t^2}}}{{{t^2} + 1}}} dt = 2\int\limits_0^1 {\left( {1 -
\frac{1}{{{t^2} + 1}}} \right)} dt =2\left ( t - \arctan x \right )
|_0^1= \boxed{\frac{{4 - \pi }}{2}} $
|
|
|
|
giải đáp
|
help me
|
|
|
|
Theo giả thiết: $\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1$
Ta có:
$P=\frac{(x-1)+(y-1)}{x^2}+\frac{(y-1)+(z-1)}{y^2}+\frac{(z-1)+(x-z)}{z^2}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$=(x-1)(\frac{1}{x^2}+\frac{1}{z^2})+(y-1)(\frac{1}{x^2}+\frac{1}{y^2})+(z-1)(\frac{1}{y^2}+\frac{1}{z^2})-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$\geq \frac{2(x-1)}{xz}+\frac{2(y-1)}{xy}+\frac{2(z-1)}{yz}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
$=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-2(\frac{1}{xz}+\frac{1}{xy}+\frac{1}{yz})=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-2 (1)$
Mà $(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})^2 \geq 3(\frac{1}{xz}+\frac{1}{xy}+\frac{1}{yz})=3 (2)$
Từ $(1)$ và $(2) \Rightarrow P \geq \sqrt{3}-2$
Kết luận: Vậy $\min P=\sqrt{3}-2 \Leftrightarrow x=y=\sqrt{3}$
|
|
|
|
giải đáp
|
Giúp với!!!
|
|
|
|
Hiển nhiên thấy $c$ và $d$ có thể chéo nhau (bao gồm cả song song, vuông góc), cắt nhau nhưng không thể trùng nhau.
|
|
|
|
giải đáp
|
những bài tập này khó wa ! giúp mình nhé !
|
|
|
|
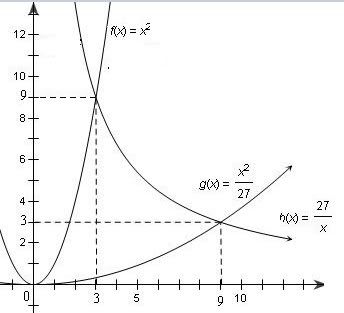 Xét các PT giao điểm : Xét các PT giao điểm :
$x^2=\frac{x^2}{27}\Leftrightarrow x=0$
$x^2=\frac{27}{x}\Leftrightarrow x=3$
$\frac{x^2}{27}=\frac{27}{x}\Leftrightarrow x=9$ $S=\int\limits_{0}^{3}(x^2-\frac{x^2}{27} ) dx+\int\limits_{3}^{9} (\frac{27}{x} -\frac{x^2}{27} )$ $=\frac{26}{27}
.\frac{x^3}{3} \mathop |\nolimits_0^3 +27\ln x\mathop |\nolimits_3^9
-\frac{1}{27} .\frac{x^3}{3} \mathop |\nolimits_3^9 =27\ln3$ (đvdt) |
|
|
|
giải đáp
|
Bất đẳng thức.
|
|
|
|
Từ giả thiết ta có thể viết lại hệ thức đã cho dưới dạng tương đương sau:
$\begin{array}{l}
{x^2} + {y^2} + {z^2} - 2yz\cos A - 2xz\cos B - 2xy\cos C \ge 0\\
\Leftrightarrow
{x^2}({\sin ^2}B + c{\rm{o}}{{\rm{s}}^2}B) + {y^2}({\sin ^2}A +
c{\rm{o}}{{\rm{s}}^2}A) + {z^2} - 2xy\cos (A + B) - 2yz\cos A\\ -
2xz\cos B \ge 0\\
\Leftrightarrow ({x^2}c{\rm{o}}{{\rm{s}}^2}B +
{y^2}c{\rm{o}}{{\rm{s}}^2}A + 2xy\cos A\cos B)\\ + ({x^2}{\sin ^2}B +
{y^2}{\sin ^2}A - 2xy\sin A\sin B) + {z^2} - 2z(y\cos A + x\cos B) \ge 0\\
\Leftrightarrow {(x\cos B + y\cos A)^2} + {(x\sin B - {\rm{y}}\sin A)^2} + {z^2} - 2z(x\cos B + {\rm{y}}\sin A) \ge 0\\
\Leftrightarrow {(x\cos B + y\cos A - z)^2} + {(x\sin B - {\rm{y}}\sin A)^2} \ge 0\\
\end{array}$
Ta có ĐPCM. |
|
|
|
giải đáp
|
Tính giới hạn ?????
|
|
|
|
Ta biết rằng $\csc x=\frac{1}{\sin x }\Rightarrow(\csc x)' = -\frac{\cos x}{\sin^ 2x}$. Do đó theo quy tắc Lopitan $\mathop {\lim }\limits_{x \to 0+}\frac{\csc x}{\ln x}=\mathop {\lim }\limits_{x \to 0+}\frac{(\csc x)' }{(\ln x)'}=\mathop {\lim }\limits_{x \to 0+}\frac{-\frac{\cos x}{\sin^ 2x}}{\frac{1}{x}}=\mathop {\lim }\limits_{x \to 0+}-\frac{x\cos x}{\sin^ 2x}$ $=\mathop {\lim }\limits_{x \to 0+}-\left (\frac{x}{\sin x}\right )^2.\cos x .\frac{1}{x}=-1.1.(+\infty)=-\infty$. |
|
|
|
giải đáp
|
giai pt dum minh đừng giải tắt quá nha
|
|
|
|
$(D)$ có VTCP: $\overrightarrow{u}=(-2,3,0)$. $(\alpha)$ có VTPT: $\overrightarrow{n}=(8,-12,0)$. Suy ra $\overrightarrow{n} = -4\overrightarrow{u}\Rightarrow \overrightarrow{n} \parallel \overrightarrow{u}\Rightarrow (D) \perp (\alpha).$ |
|
|
|
giải đáp
|
Tính tích phân
|
|
|
|
Em xem cách giải nguyên hàm tổng quát $\int\limits \sqrt{x^2+a}dx$ tại đây |
|
|
|
giải đáp
|
giải pt
|
|
|
|
Em nên xem xét kỹ vấn đề trước khi hỏi đi hỏi lại một bài |
|
|
|
giải đáp
|
CM BDT
|
|
|
|
Đặt: $x=\cos 2\alpha,\alpha \in [0,\frac{\pi}{2}]$
Suy ra:
$(1+x)^{n}+(1-x)^{n}=(1+\cos 2\alpha)^{n}+(1-\cos 2\alpha)^{n}$
$=2^{n}(\cos^{2n} (\alpha)+\sin ^{2n} (\alpha))$$\leq 2^{n}(\cos^{2} \alpha+\sin ^{2} \alpha)= 2^{n}$
$\Rightarrow$(ĐPCM)
|
|
|
|
|
|
giải đáp
|
Tìm chuỗi maclaurin
|
|
|
|
ta biết kết quả quen thuộc sau $\cos x = \sum_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}$ Suy ra $\cos^2 \frac{x}{2}=\frac{1+\cos x}{2} =\frac{1}{2}+ \frac{1}{2}\sum_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}$ |
|
|
|
giải đáp
|
GTNN giup em zoi
|
|
|
|
Ta có thể viết lại $P$ dưới dạng:
$P=(1+x)+\frac{x^2}{1-x}+(1+y)+\frac{y^2}{1-y}+\frac{1}{x+y}-2$
$=\frac{1}{1-x}+\frac{1}{1-y}+\frac{1}{x+y}-2 (1)$
Theo bất đẳng thức Côsi cơ bản ta có:
$[(1-x)+(1-y)+(x+y)](\frac{1}{1-x}+\frac{1}{1-y}+\frac{1}{x+y})\geq 9$
$\Rightarrow \frac{1}{1-x}+\frac{1}{1-y}+\frac{1}{x+y}\geq \frac{9}{2} (2)$
Từ $(1),(2)$ suy ra $P\geq \frac{5}{2} (3)$
Dấu
$"="$ trong $(3)$ xảy ra $\Leftrightarrow \begin{cases}x= y\\ 1-x=2x
\end{cases}\Leftrightarrow x=y=\frac{1}{3}$. Vậy $\min
P=\frac{5}{2}\Leftrightarrow x=y=\frac{1}{3}$.
|
|
|
|
giải đáp
|
giải hộ em
|
|
|
|
Bài toán này của em sai. Ta sẽ chứng minh: $\frac{1}{2a+b+c}+ \frac{1}{a+2b+c}+\frac{1}{a+b+2c } \le \frac{1}{4}\left ( \frac{1}{a} +\frac{1}{b}+ \frac{1}{c} \right )< \frac{1}{a} +\frac{1}{b}+ \frac{1}{c} $ * Trước hết ta chứng minh với $\forall x,y$ dương luôn có $\frac{1}{x+y} \leq \frac{1}{4x}+\frac{1}{4y} (1)$ Thật vậy: Với mọi $x,y >0 $ ta có $(x-y)^2 \geq 0 \Leftrightarrow (x+y)^2 \geq 4xy$ $\Leftrightarrow \frac{1}{x+y} \leq \frac{x+y}{xy} \Leftrightarrow \frac{1}{x+y} \leq \frac{1}{4x}+\frac{1}{4y}$ (đpcm) Theo $(1): \frac{1}{2a+b+c} \leq \frac{1}{8a}+\frac{1}{4(b+c)} \leq \frac{1}{8a}+\frac{1}{16b}+\frac{1}{16c} (2)$ Tương tự $\frac{1}{2b+c+a} \leq \frac{1}{8b}+\frac{1}{16c}+\frac{1}{16a} (3)$ $\frac{1}{2c+a+b} \leq \frac{1}{8c}+\frac{1}{16a}+\frac{1}{16b} (4)$ Cộng vế theo vế các bất đẳng thức $(2),(3),(4)$ ta có $\frac{1}{2a+b+c}+ \frac{1}{a+2b+c}+\frac{1}{a+b+2c } \leq \frac{1}{4}(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$ |
|