Bài tập này của bạn khá hay. Tôi xin nêu ra một cách để giải quyết như sau
Trước hết ta nêu ra bổ đề : Trong tất cả những tam giác nội tiếp trong một đường tròn và chung một cạnh đáy, thì tam giác cân là tam giác có diện tích lớn nhất

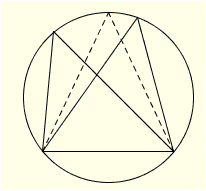
Phần chứng minh của bổ đề này là hiển nhiên vì thấy đỉnh của tam giác cân là đỉnh xa đáy nhất.
Từ đó, bài toán ban đầu có thể trở thành tìm giá trị nhỏ nhất của một tam giác cân nội tiếp đường tròn cho trước.
Giả sử ta có hình vẽ

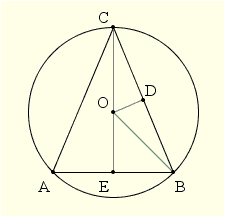
Gọi $\alpha$ là góc ở đ của tam giác cân $ABC\rightarrow \widehat{ACE}= \widehat{BCE}=90^\circ - \alpha$.
Gọi $O$ là tâm của đường tròn bán kính $R$ và $D, E$ là trung điểm của $AB, BC$.
Ta có $ \widehat{BOE}= \widehat{ACB}= 180^\circ-2\alpha\Rightarrow OE=OB. \cos \widehat{BOE}=-R \cos 2\alpha$
Do đó $CE=R(1- \cos 2\alpha)$ và $AB=2EB=2R \sin  2\alpha$.
Từ đó $S_{ABC}=\frac{1}{2}AB.CE=R^2(1- \cos 2\alpha)\sin  2\alpha=4R^2\sin \alpha\cos^3 \alpha.             (1)$
Mặt khác áp dụng BĐT Cô-si ta có
$\sin^2 \alpha\cos^6 \alpha=\frac{1}{3}.3\sin^2 \alpha.\cos^2 \alpha.\cos^2 \alpha.\cos^2 \alpha \le \frac{1}{3}\left ( \frac{3\sin^2 \alpha+\cos^2 \alpha+\cos^2 \alpha+\cos^2 \alpha}{4}\right )^4=\frac{3^3}{4^4}         (2)$
Từ $(1)$ và $(2)$ ta có $S \le \frac{3 \sqrt 3}{4}R^2$.
Như vậy $\max S = \frac{3 \sqrt 3}{4}R^2\Leftrightarrow \triangle ABC$ đều.

Bài tập này là bài tập số $26$, trang $9$, sách Bài tập hình học nâng cao $12$. Bạn có thể đọc và tham khảo tại tài liệu quen thuộc này nhé.

Nếu đúng đề bài như thế này thì bài toán có duy nhất $1$ nghiệm. Nhưng không biểu diễn dưới dạng chính xác.
Ý tưởng trong lời giải này là sử dụng phương pháp giải bậc $4$ tổng quát.
Với điều kiện $\begin{cases}2t^2-3t-1 \ge 0 \\ t^2-1 \ge 0 \end{cases}\Leftrightarrow  t \ge \frac{3+ \sqrt{17}}{4}$
PT đã cho
$\Leftrightarrow 9(t^2-1)=(2t^2-3t-1)^2$
$\Leftrightarrow 4t^4-12t^3-4t^2+6t+10=0$
$\Leftrightarrow 4t^4-12t^3+9t^2=13t^2-6t-10$
$\Leftrightarrow \left[ {t(2t-3)} \right]^2=13t^2-6t-10$
Ta thêm vào tham số $a$ như sau,
$\Leftrightarrow \left[ {t(2t-3)} \right]^2+2a.t(2t-3)+a^2=(13+4a)t^2-6(a+1)t+a^2-10$
$\Leftrightarrow (2t^2-3t+a)^2=(13+4a)t^2-6(a+1)t+a^2-10      (*)$
Đặt $f(a)=(13+4a)t^2-6(a+1)t+a^2-10$. Bây giờ giả sử $a$ là số thỏa mãn
$\Delta'_f=9(a+1)^2-(13+4a)(a^2-10)=0\Leftrightarrow 4a^3+4a^2-58a-139=0       (**)$ (nếu có nghiệm đẹp thì PT này sẽ phải có nghiệm đơn giản)
Khi đó vế phải của PT $(*)$ có nghiệm duy nhất $t=\frac{3(a+1)}{3+2a}$. Và lúc đó
$\Leftrightarrow (2t^2-3t+a)^2=(13+4a)\left (t-\frac{3(a+1)}{3+2a} \right )^2           (***)$
Chú ý rằng ràng buộc $(**)$ là ràng buộc có nghĩa vì PT bậc $3$ luôn có nghiệm, và nghiệm này được chọn thỏa mãn $13+4a>0$.
Như vậy từ $(***)$ ta thu được hai PT bậc hai và có thể giải tiếp được.

Kí hiệu
$\prod \cos A = \cos A.\cos B.\cos C$,       
$\prod \cos(B-C)= \cos(A-B).\cos(B-C). \cos(C-A)$
BĐT cần chứng minh tương đương với
$\Leftrightarrow 8\prod \cos A \le \prod \cos(B-C)$
$\Leftrightarrow 8\prod (2\cos A\sin (B+C)) \le \prod 2\sin (B+C)\cos(B-C)$
$\Leftrightarrow 8\prod (2\cos A\sin A) \le \prod (\sin 2B + \sin 2C)$
$\Leftrightarrow 8\prod \sin 2A \le \prod (\sin 2B + \sin 2C)$
Do $A, B, C$ là các góc nhọn nên $\sin 2A, \sin 2B, \sin 2C >0$ do đó
$\prod (\sin 2B + \sin 2C) \ge \prod 2\sqrt{\sin 2B\sin 2C}= 8\prod \sin 2A $ (đpcm).
Đẳng thức xảy ra $\Leftrightarrow \triangle ABC$ đều.