|
|
|
|
|
|
bình luận
|
PT chứa căn
Hãy ấn nút tam giác màu xanh bên cạnh đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
PT chứa căn
|
|
|
|
Theo mình đề bài nên sửa thành như sau
\[(x^2-6x+11)\sqrt{x^2-x+1}=2(x^2-4x+7)\sqrt{x-2}\]
Khi đó ta đặt $u=\sqrt{x^2-x+1}>0$ và $v=\sqrt{x-2}>0$, thì PT đã cho trở thành:
\[(u^2-5v^2)u=(2u^2-6v^2)v \Leftrightarrow u^3-5uv^2=2u^2v-6v^3\]
Nếu $v=0$ thì $x=2$ không phải là nghiệm ta có thể đặt $t=\frac{u}{v}$ ,ta được \[t^3-2t^2-5t+6=0\] và ta có $t=-2,1,3$
Với $t=-2$ là điều vô lý. ($u,v>0$)
Với $t=1 \Leftrightarrow u=v$ và $t=3 \Leftrightarrow u=3v$, thay trở lại $u,v$ ta được $x=5\pm\sqrt{6}$.
|
|
|
|
|
|
sửa đổi
|
PT Lượng giác vô tỷ
|
|
|
|
PT Lượng giác vô tỷ Giải phương trình$ 2\ cos ^2 x +\sqrt[3]{\sin 2x} +1=3(\sin x + \sqrt[3]{\cos x} ) $
PT Lượng giác vô tỷ Giải phương trình$ \sin x \sqrt[3]{\s in 2x } +\sqrt[3]{\sin 2x} -6=3(\sin x + \sqrt[3]{\cos x} ) $
|
|
|
|
bình luận
|
bài này e mới học chưa làm được
Nếu bạn thấy lời giải này chính xác và có ích đối với bạn. Hãy ấn vào mũi tên bên cạnh đáp án để chấp nhận và bình chọn( vote up ) nhé!
|
|
|
|
|
|
|
|
giải đáp
|
bài này e mới học chưa làm được
|
|
|
|
Đặt $t = \tan \frac{x}{2}$.
PT $\Leftrightarrow \frac{2t}{1+t^2}+\frac{1-t^2}{1+t^2}=\frac{2t}{1-t^2}\Leftrightarrow t^4-4t^3-2t^2+1=0$
$\Leftrightarrow t^4-4t^3+4t^2=6t^2-1\Leftrightarrow \left[ {t(t-2)} \right]^2=6t^2-1$
Ta thêm vào tham số $a$ như sau,
$\Leftrightarrow \left[ {t(t-2)} \right]^2+2a.t(t-2)+a^2=(6+2a)t^2-4at+a^2-1$
$\Leftrightarrow (t^2-2t+a)^2=(6+2a)t^2-4at+a^2-1 (*)$
Đặt $f(a)=(6+2a)t^2-4at+a^2-1$. Bây giờ giả sử $a$ là số thỏa mãn
$\Delta'_f=4a^2-(6+2a)(a^2-1)=0\Leftrightarrow a^3+a^2-a-3=0 (**)$
Khi đó vế phải của PT $(*)$ có nghiệm duy nhất $t=-\frac{2a}{3+a}$. Và lúc đó
$\Leftrightarrow (t^2+t+a)^2=(6+2a)\left (t+\frac{2a}{3+a} \right )^2 (***)$
Chú ý rằng ràng buộc $(**)$ là ràng buộc có nghĩa vì PT bậc $3$ luôn có nghiệm, và nghiệm này được chọn thỏa mãn $6+2a>0$.
Như vậy từ $(***)$ ta thu được hai PT bậc hai và có thể giải tiếp được.
|
|
|
|
|
|
sửa đổi
|
PT Logarit
|
|
|
|
hỏi thêm 1 câu nữa r ùi đi ngủTìm các giá trị của tham số m để phương trình sau có nghiệm $\log_5(5^x+1).\log_{25}(5^{x+1}+5)=2m+1$
PT Logari tTìm các giá trị của tham số m để phương trình sau có nghiệm $\log_5(5^x+1).\log_{25}(5^{x+1}+5)=2m+1$
|
|
|
|
sửa đổi
|
PT chứa căn
|
|
|
|
mọi người giúp tớ bài này với n héGiải phương trình $(x^2-6x+11)\sqrt{x^2+1}=2(x^2-4x+7)\sqrt{x-2} $
PT chứa căn Giải phương trình $(x^2-6x+11)\sqrt{x^2+1}=2(x^2-4x+7)\sqrt{x-2} $
|
|
|
|
bình luận
|
Tổ hợp
Hãy ấn nút tam giác màu xanh bên cạnh đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Tổ hợp
|
|
|
|
Ký hiệu các bạn nam là chấm màu đỏ, các bạn nữ là chấm màu xanh.
Xét trường hợp 1, tính từ trái qua phải thì bạn nam đứng đầu
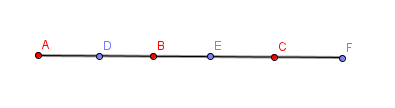
Có 3 bạn nam nên có $3!$ cách chọn vị trí sắp xếp 3 bạn này. Các bạn nữ được đặt xe kẽn và giữa khoảng cách giữa các bạn nam, nên tương tự cũng có $3!$ cách chọn vị trí sắp xếp 3 bạn nữ này. Như vậy trong trường hợp này có tổng cộng $3! \times 3!=36$ cách sắp xếp thỏa mãn bài toán.
Tương tự cho trường hợp 2, tính từ trái qua phải thì bạn nữ đứng đầu thì cũng có 36 cách sắp xếp thỏa mãn bài toán.
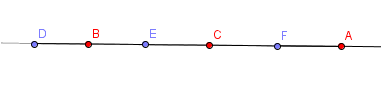
Vậy tóm lại ta có $36+36=72$ cách sắp xếp thỏa mãn bài toán.
|
|
|
|
sửa đổi
|
Bất đẳng thức dạng tổng quát với n
|
|
|
|
th êm bài n ày n ữa n hécho $x, y, z$ là số dương thỏa mãn $xyz=1$ và $n$ là số nguyên dương. CMR: $M=\frac{x^n}{y+z}+\frac{y^n}{z+x}+\frac{z^n}{x+y}\geq \frac{3}{2} $
Bất đẳng th ức dạn g tổn g quát với n cho $x, y, z$ là số dương thỏa mãn $xyz=1$ và $n$ là số nguyên dương. CMR: $M=\frac{x^n}{y+z}+\frac{y^n}{z+x}+\frac{z^n}{x+y}\geq \frac{3}{2} $
|
|
|
|