Ta có
      $a\tan A+b\tan B=(a+b)\cot\frac{C}{2} $
$\Leftrightarrow a\tan A+b\tan B=(a+b)\tan\frac{A+B}{2} $
$\Leftrightarrow a\left (\tan A- \tan\frac{A+B}{2} \right )+b\left (\tan B- \tan\frac{A+B}{2} \right )=0$
$\Leftrightarrow \displaystyle{a\frac{\sin\frac{A-B}{2}}{\cos A \cos \frac{A+B}{2}}-b\frac{\sin\frac{A-B}{2}}{\cos B \cos \frac{A+B}{2}}}=0$
$\Leftrightarrow \left[ \begin{matrix} \sin\frac{A-B}{2}=0          (1)\\ \frac{a}{\cos A}-\frac{b}{\cos B}=0        (2)\end{matrix}\right.$
$(1)\Leftrightarrow A=B \Leftrightarrow \triangle ABC$ cân.
$(2)\Leftrightarrow\frac{a}{\cos A}=\frac{b}{\cos B}=0\Leftrightarrow \frac{a}{\frac{b^2+c^2-a^2}{2bc}}=\frac{b}{\frac{a^2+c^2-b^2}{2ac}} \Leftrightarrow b^2+c^2-a^2=a^2+c^2-b^2\Leftrightarrow a=b \Leftrightarrow \triangle ABC$ cân.

PT
$\Leftrightarrow x^4-(k^2x^2-2kx+1)=0$
$\Leftrightarrow x^4-(kx-1)^2=0$
$\Leftrightarrow (x^2+kx-1)(x^2-kx+1)=0$
$\Leftrightarrow \left[ {\begin{matrix} x^2+kx-1=0\\x^2-kx+1=0\end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x_1=\frac{1}{2}\left ( -k+\sqrt{k^2+4}\right )\\x_2=\frac{1}{2}\left ( -k-\sqrt{k^2+4}\right )\\x_3=\frac{1}{2}\left ( k+\sqrt{k^2-4}\right )\\x_4=\frac{1}{2}\left ( k-\sqrt{k^2-4}\right )\end{matrix}} \right.$
Từ đây nhận thấy với $|k| >2$ và  thì PT đã cho có $4$ nghiệm phân biệt.

Chúng ta còn một cách tiếp cận khác khi tìm ra
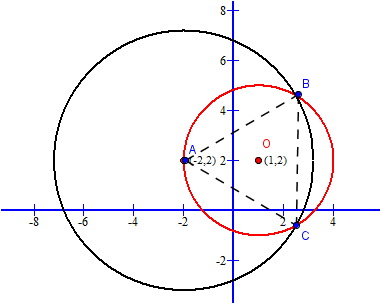
$(C): (x-1)^2+(y-2)^2=9 \Rightarrow (C)$ là đường tròn tâm $O(1,2)$, bán kính $3 $ và $A\in (C)$.
Tam giác đều $ABC$ nội tiếp đường tròn bán kính $R=3$ nên cạnh của tam giác đều là
$AB=AC=BC=R\sqrt 3= 3 \sqrt 3$  (bạn đọc tự lý giải điều này nhé.)
Lúc này $B, C$ là giao điểm của hai đường tròn tâm $O(1,2)$, bán kính $3 $ và đường tròn tâm $A(-2,2)$, bán kính $3\sqrt 3 $ nên tọa độ của $B, C$ là nghiệm của hệ
      $\begin{cases}(x-1)^2+(y-2)^2=9 \\ (x+2)^2+(y-2)^2=27 \end{cases} \Leftrightarrow \begin{cases}(x+2)^2-(x-1)^2=18 \\ (x+2)^2+(y-2)^2=27 \end{cases}$
$\Leftrightarrow \begin{cases}6x=15 \\ (x+2)^2+(y-2)^2=27 \end{cases}\Leftrightarrow \begin{cases}x=\frac{5}{2} \\ y=2\pm \frac{3\sqrt{3}}{2} \end{cases}$
Như vậy  $B\left(\frac{5}{2},2+ \frac{3\sqrt{3}}{2}\right);  C\left(\frac{5}{2},2- \frac{3\sqrt{3}}{2}\right)$.

Bài toán này còn có thể làm "chặt" bởi bất đẳng thức sau :
Cho tam giác $ABC$ nhọn.  Chứng minh rằng  $\sin A+\sin B+\sin C \le \frac{3 \sqrt 3}{2}$.
Trước hết ta chứng minh bài toán phụ sau,
Với $0< x,y < \frac{\pi}{2}$    thì    $\sin x + \sin y \le 2 \sin \frac{x+y}{2}$.
Thật vậy,
$\sin x + \sin y = 2 \sin \frac{x+y}{2} \cos \frac{x-y}{2} \le 2 \sin \frac{x+y}{2}$.
Đẳng thức xảy ra $\Leftrightarrow \cos \frac{x-y}{2}=1 \Leftrightarrow x=y.$
Bây giờ áp dụng BĐT này ta có
$\begin{cases}\sin A + \sin B \le 2 \sin \frac{A+B}{2}\\ \sin C + \sin \frac{\pi}{3} \le 2 \sin \frac{C+\frac{\pi}{3}}{2} \\ 2 \sin \frac{A+B}{2}+2 \sin \frac{C+\frac{\pi}{3}}{2}  \le 4 \sin \frac{A+B+C+\frac{\pi}{3}}{4}=4\sin\frac{\pi}{3} \end{cases}$
Cộng theo từng vế ba BĐT trên ta có
$\sin A+\sin B+\sin C \le 3\sin\frac{\pi}{3}=\frac{3 \sqrt 3}{2}$, đây là đpcm.
Đẳng thức xảy ra $\Leftrightarrow A=B=C \Leftrightarrow \triangle ABC$ đều.
Rõ ràng trong trường hợp này thì $\frac{3 \sqrt 3}{2} < \pi $ nên ta có kết luận của bài toán ban đầu.