c) Ta biết rằng hai mặt phẳng không song song với nhau thì cắt nhau theo một giao tuyến là đường thẳng. Vì thế để xác định đường thẳng này thì ta chỉ cần tìm hai điểm mà đều thuộc cả hai mặt phẳng.
Thứ nhất nếu gọi $A'B$ cắt $AB'$ tại $M$, thì $M$ là trung điểm của hai đoạn thẳng này và suy ra nó đều trên hai mặt phẳng $(AB'C')$ và $(A'BC)$.
Thứ hai nếu gọi $A'C$ cắt $AC'$ tại $N$, thì $N$ là trung điểm của hai đoạn thẳng này và suy ra nó đều trên hai mặt phẳng $(AB'C')$ và $(A'BC)$.
Theo tính chất của đường trung bình thì $MN$ đi qua $O$ xác đinh từ câu b), và giao tuyến cần tìm chính là đường thẳng $MN$.

b) Trong mặt phẳng $A'I'IA$ gọi giao điểm của hai đường thẳng $A'I$ và $AI'$ là $O$ thì $O$ là trung điểm của mỗi đoạn vì đây là hình bình hành.
Điểm $O$ thuộc $AI'$ nên nó cũng nằm trong mặt phẳng $(AB'C')$.
Vì vậy giao điểm của $A'I$ và mặt phẳng $(AB'C')$ chính là điểm $O$.

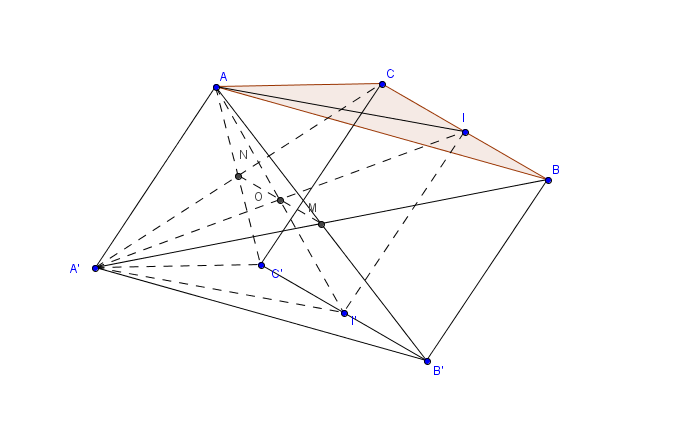a) Do các mặt bên của hình lăng trụ đều là hình bình hành, nói riêng với mặt $BCC'B'$ có $I, I'$ lầ lượt là trung điểm của $BC,B'C;$ nên $II' \parallel BB', II'=BB'.$
Mặt khác cũng có $BB' \parallel AA', BB'=AA'.$
Do đó $II' \parallel AA', II'=AA'.$
Suy ra $AA'I'I$ là hình bình hành và $AI \parallel A'I, AI'=A'I'.$

Điều kiện $\sin 2x \ne 0.$
PT $\Leftrightarrow 2 \cos2x\cos \frac{\pi}{4}-2 \sin2x\sin \frac{\pi}{4}=\frac{\cos x}{\sin x}-\frac{\sin x}{\cos x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{\cos^2x-\sin^2 x}{\sin x\cos x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{2\cos2x}{\sin 2x}-2$
$\Leftrightarrow \sqrt 2\left (  \cos2x-\sin 2x \right )=\frac{2(\cos2x-\sin 2x)}{\sin 2x}$
$\Leftrightarrow \left[ {\begin{matrix} \cos2x=\sin 2x\\ \sin 2x=\frac{1}{\sqrt 2} \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} \cot2x=1\\ \sin 2x=\frac{1}{\sqrt 2} \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x=\frac{\pi}{8}+k\frac{\pi}{2}\\ x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{8}+k\pi \\\end{matrix}} \right.     (k \in \mathbb{Z}).$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

1.
+ Tìm GTLN
Với mọi $x$ ta đều có
$(x+2012)^2 \ge 4.2012.x=8048x\Leftrightarrow \frac{x}{(x+2012)^2} \le \frac{1}{8048}$
Vậy GTLN là $\frac{1}{8048}$ đạt tại khi $x=2012.$
+ Tìm GTNN
Thấy rằng $(x+2012)^2 >0$ và khi $x \to - \infty$ thì biểu thức mang giá trị $- \infty$.
Vậy không tồn tại GTNN.

Áp dụng công thức
$(x_1+x_2+\cdots+x_m)^n=\sum_{k_1+k_2+\cdots+k_m=n}\left ( \begin{matrix} n\\k_1,k_2,\cdots,k_m \end{matrix} \right )\prod_{1 \le t \le m}x_t^{k_t}$
Trong đó $\left ( \begin{matrix} n\\k_1,k_2,\cdots,k_m \end{matrix} \right )=\frac{n!}{k_1!.k_2!\cdots k_m!}$ và  $ k_1,k_2,\cdots,k_m \in \mathbb{N}$.
Áp dụng vào bài này với $m=4, n=20, k_1=5, k_2=3, k_3=k_4=6.$
Ta có đáp số là
$\frac{20!}{5!.3!6!6!}=6 518 191 680$

b)
PT đường thẳng  $AN: y=\frac{1}{4}nx+\frac{1}{2}n $
PT đường thẳng  $BM: y=-\frac{1}{4}mx+\frac{1}{2}m $
Điểm $I$ là giao điểm của hai đường thẳng trên nên $\begin{cases}x_I=\frac{2(m-n)}{m+n} \\ y_I= \frac{mn}{m+n}\end{cases}   (m+n \ne 0)$
Với $mn=1$ thì $x_I^2+16y_I^2=4$
Vậy $I$ chạy trên Elip có PT $\left ( \frac{x}{2} \right )^2+\left ( \frac{y}{\frac{1}{2}} \right )^2=1$

b) Để $4$ viên có $3$ màu thì có các trường hợp
Chọn được $2$ viên đỏ có $C_7^2$ cách, hai viên còn lại chọn trong $6$ xanh, $5$ trắng có $5 \times 6$ cách.
Chọn được $2$ viên xanh có $C_6^2$ cách, hai viên còn lại chọn trong $7$ đỏ, $5$ trắng có $5 \times 7$ cách.
Chọn được $2$ viên trắng có $C_5^2$ cách, hai viên còn lại chọn trong $6$ xanh, $7$ đỏ có $7 \times 6$ cách.
Vậy đáp số cần tìm là:
$\frac{5 \times 6\times C_7^2+5 \times 7\times C_6^2+7 \times 6\times C_5^2}{C_{18}^4}=\frac{35}{68}$

a) Để $4$ viên cùng màu thì xác suất là
$\frac{C_5^4+C_6^4+C_7^4}{C_{18}^4}=\frac{11}{612}$

Để cả $3$ quả đều khác màu nhau thì có xác suất là
$\frac{C_5^1C_6^1C_4^1}{C_{15}^3}=\frac{24}{91}$

a)
$\textbf{ Nhắc lại}$
Đường thẳng $Ax+By+C=0   (A^2+B^2 >0)$ tiếp xúc với elip $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ khi và chỉ khi $C^2=A^2a^2+B^2b^2$.

Tiếp đến viết PT đường thẳng $MN : x(m-n)+4y-2(m+n)=0$
Ta cần có $\Leftrightarrow 4(m+n)^2=4(m-n)^2+16\Leftrightarrow \boxed{mn=1}.$

Trước hết ta tìm xác suất để chọn ra $3$ bạn đều là nữ. Đó là $\frac{C_7^3}{C_{12}^3}$
Và suy ra xác suất để chọn ít nhất một nam là   $1-\frac{C_7^3}{C_{12}^3}=\frac{37}{44}$

Đặt
$\begin{cases}a=2x+\sqrt{x+1}+1 \\ b=2x-\sqrt{x+1}\end{cases}\Rightarrow 2\sqrt{x+1}+1=a-b$
Do đó HPT ban đầu
$\Leftrightarrow \sqrt{a}+\sqrt{b}=a-b$
$\Leftrightarrow \sqrt{a}+\sqrt{b}=(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$
$\Leftrightarrow \sqrt{a}-\sqrt{b}=1$
Như vậy ta có
$\begin{cases}\sqrt{a}+\sqrt{b}=a-b=2\sqrt{x+1}+1 \\  \sqrt{a}-\sqrt{b}=1 \end{cases}$
Cộng theo từng vế hai PT này ta được
      $\sqrt{a}=\sqrt{x+1}+1$
$\Leftrightarrow \sqrt{2x+\sqrt{x+1}+1}=\sqrt{x+1}+1$
$\Leftrightarrow 2x+\sqrt{x+1}+1=x+2+2\sqrt{x+1}$
$\Leftrightarrow x-1=\sqrt{x+1}$
$\Leftrightarrow \begin{cases}x\ge 1 \\ (x-1)^2=x+1 \end{cases}$
$\Leftrightarrow \begin{cases}x\ge 1 \\ x(x-3)=0 \end{cases}$
$\Leftrightarrow \boxed{x=3}$  (thỏa mãn).