|
|
giải đáp
|
giải hê
|
|
|
|
HPT $\Leftrightarrow \begin{cases}(x-1)(y-1)(x+y-2)=6\\(x-1)^2+(y-1)^2=1\end{cases} $
$\underbrace{\Leftrightarrow}_{\begin{matrix} a=x-1\\
b=y-1 \end{matrix}}\begin{cases}ab(a+b)=6\\a^2+b^2=5\end{cases}\Leftrightarrow \begin{cases}ab=\frac{6}{a+b}\\(a+b)^2-2ab=5\end{cases}\Leftrightarrow \begin{cases}ab=\frac{6}{a+b}\\(a+b)^2-\frac{12}{a+b}=5\end{cases}$
$\Leftrightarrow \begin{cases}ab=\frac{6}{a+b}\\(a+b)^3-5(a+b)-12=0\end{cases}\Leftrightarrow \begin{cases}ab=2 \\ a+b= 3\end{cases}\Leftrightarrow\left[ {\begin{matrix} \begin{cases}a=2 \\ b= 1\end{cases}\\ \begin{cases}a=1 \\ b= 2\end{cases} \end{matrix}} \right.$
Vậy $\boxed{(x, y) \in \left\{ {(2;3), (3;2)} \right\}}$.
|
|
|
|
giải đáp
|
chứng minh
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
TOÁN 11
|
|
|
|
b) Gọi $D $ là điểm đối xứng của $B $ qua $A$.
Xét phép quay $Q_A$ tâm $A$ góc quay $90^\circ$ chiều dương là chiều ngược chiều kim đồng hồ.
$Q_A : D \to N, C \to Q$
suy ra $DC=NQ, DC \perp NQ.$
Mặt khác dễ thấy $AM$ là đường trung bình của $\triangle BCD$.
Từ đây có đpcm.
|
|
|
|
giải đáp
|
tìm GTLN
|
|
|
|
Áp dụng BĐT Cô-si ta có
$\underbrace{a^{2009}+\cdots+a^{2009}}_{4 \text {số}}+\underbrace{1+\cdots+1}_{2005 \text {số}} \ge 2009\sqrt[2009]{a^{4.2009}}=2009a^{4}$
Suy ra $4.a^{2009}+2005 \ge 2009a^4$
Tương tự ta cũng có
$4.b^{2009}+2005 \ge 2009b^4$
$4.c^{2009}+2005 \ge 2009c^4$
Cộng theo từng vế ba BĐT này ta được
$4\left (a^{2009}+b^{2009}+c^{2009} \right )+3.2005 \ge 2009\left (a^4+b^4+c^4 \right )$
$\Leftrightarrow 12+3.2005 \ge 2009\left (a^4+b^4+c^4 \right )$
$\Leftrightarrow 3 \ge a^4+b^4+c^4$
Vậy $\max P=3\Leftrightarrow a=b=c=1.$
|
|
|
|
giải đáp
|
gpt
|
|
|
|
PT $\Leftrightarrow 2\sin x \cos x -3(1-\cos x)=0\Leftrightarrow 4\sin \frac{x}{2}\cos \frac{x}{2}\cos x-6\sin^2\frac{x}{2}=0$ Nếu $\sin \frac{x}{2}=0\Leftrightarrow x=k2\pi/$ Nếu $\sin \frac{x}{2} \ne 0 \Rightarrow 2\cos \frac{x}{2}\cos x=3\sin\frac{x}{2}\Rightarrow 2\cos x=3\tan \frac{x}{2}$ Đặt $t=\tan \frac{x}{2}$ thì PT trên trở thành $\frac{2(1-t^2)}{1+t^2}=3t\Leftrightarrow 3t^3+2t^2+3t-2=0$ Đây là pt bậc ba có nghiệm duy nhất nhưng không đẹp, có thể giải bằng pp Cardano $t$ 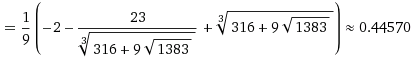 |
|
|
|
giải đáp
|
phép biến hình lớp 11
|
|
|
|
 Gọi $O$ là tâm hình vuông. Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$ do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$. Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$ do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có $MN=M'N'$ và $MN \bot M'N'$ Theo giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$. |
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
 Gọi $O$ là tâm hình vuông. Ta có:$Q(O,90^\circ): B\rightarrow A, A\rightarrow D,$ do đó, qua phép quay này, đường thẳng $BA$ biến thành đường thẳng $AD$ và $M \in AB \rightarrow M'\in AD, N\rightarrow N'$. Ta cũng có: $Q(O,90^\circ): C\rightarrow B; D\rightarrow C,$ do đó, qua phép quay này, đường thẳng $CD$ biến thành đường thẳng $BC$ và $N\rightarrow N'$. Theo tính chất của phép quay ta có $MN=M'N'$ và $MN \bot M'N'$ Theo
giả thiết $MN\bot PQ$ vì vậy hoặc $PQ \parallel M'N'$ hoặc $PQ \equiv
M'N'$. Trong cả hai trường hợp, ta đều suy ra được $MN=PQ$. |
|
|
|
giải đáp
|
TOÁN 11
|
|
|
|
a) Xét phép quay $Q_A$ tâm $A$ góc quay $90^\circ$ chiều dương là chiều ngược chiều kim đồng hồ.
$Q_A : N \to B, C \to Q$
suy ra $CN=BQ, CN \perp BQ.$
|
|
|
|
giải đáp
|
Phương trình lượng giác.
|
|
|
|
PT $\Leftrightarrow \cos 3x=\sin 5x \Leftrightarrow \cos 3x= \cos \left ( \frac{\pi}{2} -5x\right )$
$\Leftrightarrow \left[ {\begin{matrix} 3x= \frac{\pi}{2} -5x+k2\pi\\ 3x=- \frac{\pi}{2} +5x+k2\pi \end{matrix}} \right.$
$\Leftrightarrow \left[ {\begin{matrix} x= \frac{\pi}{16}+k\frac{\pi}{4}\\ x= \frac{\pi}{4} -k\pi \end{matrix}} \right. (k \in \mathbb{Z}).$
|
|
|
|
giải đáp
|
Nhị thức Newton
|
|
|
|
Trước hết bạn chứng minh công thức sau coi như bài tập nhé
$C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$
Áp dụng công thức này ta có
$S=\left (C_{29}^{13}+C_{29}^{14} \right )-\left (C_{29}^{14}+C_{29}^{15} \right )+\left (C_{29}^{15}+C_{29}^{16} \right )-\cdots+\left (C_{29}^{27}+C_{29}^{28} \right )-\left (C_{29}^{28}+C_{29}^{29} \right )+C_{29}^{29}$
$S=C_{29}^{13}$
|
|
|
|
giải đáp
|
cho tam giác ABC
|
|
|
|
Theo định lí $\sin $ ta có:
$(a-b) \cot \frac{ C}{ 2} =2R(\sin A - \sin B) \cot \frac{ C}{ 2} = 4R \cos \frac{ A+B}{ 2} \sin \frac{ A-B}{ 2}. \frac{ \cos \frac{ C}{ 2} }{ \sin \frac{ C}{ 2} } $
Vì : $\cos \frac{ A+B}{ 2} = \sin \frac{ C}{ 2} \neq 0 , \cos \frac{C }{2 } = \sin \frac{ A+B}{ 2} $
nên $(a-b)\cot \frac{ C}{ 2} = 2R(\cos B- \cos A) (2)$
Tương tự : $(b-c)\cot \frac{A }{ 2} = 2R(\cos C- \cos B) ( 3)$
$(c-a)\cot \frac{ B}{ 2} = 2R(\cos A- \cos C) ( 4)$
Cộng vế với vế của $(2) , (3) , (4)$ với nhau ta được
$VT (1) = 2R(\cos B- \cos A+\cos C- \cos B+\cos A-\cos C)=0 = VP (1)$
|
|
|
|
giải đáp
|
bdt nữa nào
|
|
|
|
Bài này thuộc dạng cơ bản
BĐT đã cho
$\Leftrightarrow 3(x^2+y^2+z^2)-(x+y+z)^2 \ge 0$
$\Leftrightarrow (x-y)^2+(y-z)^2+(z-x)^2 \ge 0$
BĐT này hiển nhiên đúng với mọi $x, y, ,z.$
Đẳng thức xảy ra $\Leftrightarrow x=y=z.$
|
|
|
|
giải đáp
|
tính nguyên hàm
|
|
|
|
Trước hết ta có
$1=(\sin^2 x +\cos^2 x)^2=\sin^4 x+\cos^4 x +2\sin^2 x \cos^2 x=\sin^4 x+\cos^4 x +2\sin^2 x \cos^2 x(\sin^2 x +\cos^2 x)$
$=\sin^4 x(1+2\cos^2 x)+\cos^4 x (1+2\sin^2 x)=\sin^4 x(1+2\cos^2 x)+\cos^4 x (\cos^2 x+3\sin^2 x)$
$=\cos^6x+\sin^4 x+2\sin^4 \cos^2 x+3\sin^2 x\cos^4 x$
Suy ra
$\frac{1}{\sin^3x\cos^5x}=\frac{\cos^6x+\sin^4 x+2\sin^4 \cos^2 x+3\sin^2 x\cos^4 x}{\sin^3x\cos^5x}=\frac{\cos x}{\sin^3 x}+\frac{\sin x}{\cos^5 x}+\frac{2\sin x}{\cos^3 x}+\frac{3}{\sin x \cos x}$
$\Rightarrow \int\limits\frac{1}{\sin^3x\cos^5x}dx=\int\limits\frac{\cos x}{\sin^3 x}dx+\int\limits\frac{\sin x}{\cos^5 x}dx+\int\limits\frac{2\sin x}{\cos^3 x}dx+\int\limits\frac{3}{\sin x \cos x}dx$
$\Rightarrow \int\limits\frac{1}{\sin^3x\cos^5x}dx=\int\limits\frac{d(\sin^2
x)}{2\sin^4 x}-\int\limits\frac{d(\cos^4 x)}{4\cos^8
x}-\int\limits\frac{d(\cos^2 x)}{\cos^4
x}+3\int\limits\frac{d(\tan x)}{\tan x}$
Vậy
$\boxed{\displaystyle{ \int\limits\frac{1}{\sin^3x\cos^5x}dx=-\frac{1}{2\sin^2x}+\frac{1}{4\cos^4x}+\frac{1}{\cos^2x}+3\ln|\tan x|+C}}$
|
|
|
|
giải đáp
|
Số hữu tỉ
|
|
|
|
Bài toán này không đúng.
Với $p=q=2, r=-1$ là các số hữu tỷ.
PT trên trở thành $3x^2-4x+3=0$
có nghiệm $x=\frac{1}{3}\left ( 4 \pm \sqrt 7\right )$ không là số hữu tỷ.
|
|
|
|
giải đáp
|
cần gấp giải= toán cao cấp 2
|
|
|
|
3) Trước hết ta sẽ chứng minh BĐT phụ sau
Với $x>0$ thì $f(x)=2e^x-x^2>0$.
Thật vậy, $f'(x)=2e^x-2x, f''(x)=2e^x-2>0\Rightarrow f'$ đồng biến $\Rightarrow f'(x)>f'(0)=2>0$
$\Rightarrow f$ đồng biến $\Rightarrow f(x)>f(0)=2>0$.
Tóm lại $2e^x>x^2\Rightarrow \frac{e^{2x}}{x^2}=\left ( \frac{e^{x}}{x} \right )^2>\frac{x^2}{4}$
$\Rightarrow \mathop {\lim }\limits_{x \to +\infty} \frac{e^{2x}}{x^2} = +\infty$
|
|