|
|
giải đáp
|
đố mọi người nha
|
|
|
|
b) Tập hợp các điểm $M(x,y)$ thỏa mãn bài toán là tập hợp các điểm có cả hai tọa độ đều nguyên, $x, y \in \mathbb{Z}$ và nằm trong phần mặt phẳng được kẻ ngang như trong hình vẽ câu a.
|
|
|
|
giải đáp
|
đố mọi người nha
|
|
|
|
a) Viết lại BPT dưới dạng $y \le 4-\frac{4}{3}x$. Nhận thấy rằng gốc tọa độ $O(0,0)$ thỏa mãn PT này nên tập hợp các điểm biểu diễn là nửa mặt phẳng chứa điểm $O$ và có bờ là đường thằng $y=4-\frac{4}{3}x$ như hình vẽ. 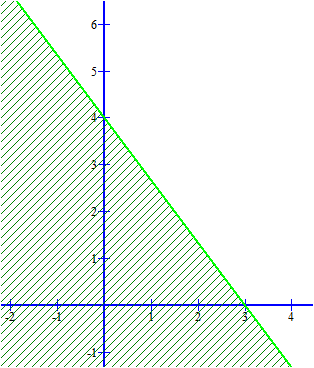 |
|
|
|
giải đáp
|
Giải các bất phương trình :
|
|
|
|
2)
PT $\Leftrightarrow {{\log }_{\frac{1}{2}}}{{\log }_2}\left(
{{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)<0\Leftrightarrow
{{\log }_2}\left( {{3^{2{{\log }_3}x - 3x + {{\log }_3}9}}} \right)>1$
$\Leftrightarrow 3^{2{{\log }_3}x - 3x + {{\log }_3}9}>2\Leftrightarrow 2{{\log }_3}x - 3x + {{\log }_3}9>\log_32$
$\Leftrightarrow 2{{\log }_3}x -3x+2-\log_32>0$
Xét hàm số $f(x)= 2{{\log }_3}x -3x+2-\log_32$
có $f'(x)=\frac{2}{x \ln 3}-3=0\Leftrightarrow x=\frac{2}{3 \ln 3}$
Lập bảng biến thiên của $f(x)$ ta thấy rằng $f(x) \le f(\frac{2}{3 \ln 3})<0$.
Vì thế BPT đã cho vô nghiệm.
|
|
|
|
giải đáp
|
Giải bất phương trình :
|
|
|
|
1) Điều kiện $x^2-x-6 >0\Leftrightarrow x>3$ hoặc $x<-2.$
Do $8/3>1$ nên theo tính chất của Lôgarit nên
BPT $\Leftrightarrow {\log _{\frac{1}{{2}}}}\left( {x^2-x-6 } \right) \ge 1$
Do $1/2<1$ nên theo tính chất của Lôgarit nên
BPT
$\Leftrightarrow x^2-x-6 \le \frac{1}{2}\Leftrightarrow
\frac{1}{2}\left ( 1+3\sqrt 3 \right )\ge x>3$ hoặc $
\frac{1}{2}\left ( 1-3\sqrt 3 \right )\le x<-2.$
|
|
|
|
giải đáp
|
Giải bất phương trình :
|
|
|
|
1) Điều kiện $x^2-4x+3 >0\Leftrightarrow x>3$ hoặc $x<1.$
Do $3>1$ nên theo tính chất của Lôgarit nên
BPT $\Leftrightarrow {\log _{\frac{9}{{16}}}}\left( {{x^2} - 4x + 3} \right) \le 1$
Do $9/16<1$ nên theo tính chất của Lôgarit nên
BPT $\Leftrightarrow {x^2} - 4x + 3 \ge \frac{9}{16}\Leftrightarrow (4x-3)(4x-13) \ge 0\Leftrightarrow x\ge \frac{13}{4}>3$ hoặc $ x\le \frac{3}{4}<1.$
|
|
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
3) Điều kiện $x >0$. Do $1/2<1$ nên ta có
BPT $\Leftrightarrow
3{\log _{\frac{1}{2}}}x < 1\Leftrightarrow {\log _{\frac{1}{2}}}x
< 1/3\Leftrightarrow x>(1/2)^{1/3}=\frac{1}{\sqrt[3]{2}}$
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
2) Điều kiện $1/3 >x >-5$.
BPT $\Leftrightarrow {\log _5}\left( {x + 5} \right) + {\log _5}(1 - 3x) > 1$
$\Leftrightarrow {\log _5}\left( {x + 5} \right)(1 - 3x) > 1$
$\Leftrightarrow\left( {x + 5} \right)(1 - 3x)>5 $
$ \Leftrightarrow x(3x+14)<0$
$\Leftrightarrow -14/3 <x<0 $
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
1) ĐK: $x\in (0,20)\backslash \{ 1\} $
$\log_x{\sqrt{20-x}}<1
\Leftrightarrow \begin{cases} 0<x<1 \\ x>\sqrt{20-x}
\end{cases} \vee \begin{cases} 1<x<20 \\ x<\sqrt{20-x}
\end{cases}$
$\Leftrightarrow \begin{cases} 0<x<1 \\
x<-5\vee x>4 \end{cases} \vee \begin{cases} 1<x<20 \\
-5<x<4\end{cases} \Leftrightarrow 1<x<4$.
|
|
|
|
giải đáp
|
Giải các bất phương trình :
|
|
|
|
1)
Điều kiện $x >0$. do $1/2<1$ nên
BPT
$\Leftrightarrow\log _{\frac{1}{2}}{\left( {\frac{1}{2}} \right)^{\log
_{\frac{1}{2}}^2x}}\le \log _{\frac{1}{2}}x^3\Leftrightarrow {\log
_{\frac{1}{2}}^2x}\le3{\log _{\frac{1}{2}}x}\Leftrightarrow0\le\log
_{\frac{1}{2}}x\le3\Leftrightarrow 1/8\le x\le1$.
|
|
|
|
giải đáp
|
Giúp em bài này
|
|
|
|
2)
Điều kiện $x >0, x\ne 1$.
BPT $\Leftrightarrow
\log{x^{\frac{1}{{\log x}}}}> \log10x^4\Leftrightarrow 1>1+4\log x\Leftrightarrow \log x<0\Leftrightarrow 0<x<1$.
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
2) BPT $\Leftrightarrow (3^x)^2-2.3^x-3 <0\Leftrightarrow (3^x-3)(3^x+1)<0\Leftrightarrow 3^x <3\Leftrightarrow x<1$.
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
1) BPT $\Leftrightarrow (\log_2 x -1)(\log_2 x -2) \ge 0\Leftrightarrow \left[ {\begin{matrix} \log_2 x \ge 2\\ \log_2 x \le 1 \end{matrix}} \right.\Leftrightarrow \left[ {\begin{matrix} x \ge 4\\ 0 < x <1 \end{matrix}} \right.$
|
|
|
|
giải đáp
|
Giúp em bài này
|
|
|
|
1)
Điều kiện $x >0, x\ne 1$.
BPT $\Leftrightarrow
\log_2{x^{{{\log }_2}x}} < \log_232\Leftrightarrow (\log_2x)^2\le
5\Leftrightarrow -\sqrt 5 \le \log_2 x \le \sqrt 5\Leftrightarrow
2^{-\sqrt 5} \le x \le 2^{\sqrt 5}, x \ne 1$.
|
|
|
|