Ta xét
$\left(\frac{1+\sqrt{3}}{2}\right)(a^2+b^2+c^2)-(ab+bc+2ca)=$ $(a-c)^2+\frac{\sqrt{3}-1}{2}\left(\left(\frac{\sqrt{3}+1}{2}\right)b-a\right)^2+\frac{\sqrt{3}-1}{2}\left(\left(\frac{\sqrt{3}+1}{2}\right)b-c\right)^2\geq0$       $(1)$
Do đó  $ab+bc+2ca\leq \frac{1+\sqrt{3}}{2}$.
Vậy $\max P=\frac{1+\sqrt{3}}{2}$.
Các giá trị $a, b, c$ được tìm từ $(1)$ và điều kiện ban đầu.

Đề bài của bạn không có PT của $d_1. d_2$ nên mình chỉ cho bài này tương tự để bạn tham khảo nhé
http://toan.hoctainha.vn/Thu-Vien/Bai-Tap/106887/bai-106887

$\textbf{Cách 2}$
Đặt $a=\sqrt[3]{6x-3x^2}$ ta được hệ

$\begin{eqnarray}x^3-x-3 &=& 2a\\6x-3x^2 &=& a^3\end{eqnarray}$

Cộng theo từng vế ta có

$x^3-3x^2+5x-3=a^3+2a            (1)$

$\Leftrightarrow (x-1)^3+2(x-1)=a^3+2a$

Đặt  $y =x-1$ ta được

$y^3+2y=a^3+2a$

$\Leftrightarrow (y-a)(y^2+ay+a^2+2)=0$
Dễ thấy  $y^2+ay+a^2+2>0\Rightarrow y=a\iff a=x-1$

Từ  $(1)$ suy ra $x^3-x-3=2x-2\iff x^3-3x=1$

Đặt  $x=2t$ ta có

$8t^3-6t=1\iff 4t^3-3t={1\over 2}$

Suy ra tồn tại $\phi$ thỏa mãn  $t=\cos\phi$, do đó

$\cos 3\phi={1\over 2}\iff 3\phi=\pm{\pi\over 3}+2k\pi\iff \phi=\pm{\pi\over 9}+{2k\pi\over 3},k\in\mathbb{Z}$

Và  $x=2\cos\phi=2\cos\left(\pm{\pi\over 9}+{2k\pi\over 3}\right)$,

Vậy $x\in\left\{2\cos{\pi\over 9},2\cos{5\pi\over 9},2\cos{7\pi\over 9}\right\}$.

Bài này nghiệm không đơn giản nên mình đưa ra cách giải như sau
PT $\Leftrightarrow (x^3 - x -3)^3=8(6x-3x^2)\Leftrightarrow (x^3 - x -3)^3-8(6x-3x^2)=0$
$\Leftrightarrow x^9-3x^7-9x^6+3x^5+18x^4+26x^3+15x^2-75x-27=0$
$\Leftrightarrow (x^3-3x-1)(x^6-8x^3+3x^2-6x+27)=0$
Kiểm tra rằng PT $x^6-8x^3+3x^2-6x+27=(x^3-4)^2+3(x-1)^2+8>0$.
Nên $x^3-3x=1                (1)$.
Nếu $|x| >2$ thì $|x|(|x|^2-3) >1$. Vô lý với (1).
Với $|x| \le 2$ thì đặt $x=2\cos \alpha$ và $(1)\Leftrightarrow 4\cos^3 \alpha-3\cos \alpha=1/2\Leftrightarrow \cos 3\alpha=1/2$
$\iff 3\alpha=\pm{\pi\over 3}+2k\pi\iff \alpha=\pm{\pi\over 9}+{2k\pi\over 3},k\in\mathbb{Z}$
Vậy  $x\in\left\{2\cos{\pi\over 9},2\cos{5\pi\over 9},2\cos{7\pi\over 9}\right\}$.

Đặt $t=\tan \frac{x}{2}, t\ne 0, t\ne \pm 1$ .
thì $\tan x=\frac{2t}{1-t^2}, \sin x=\frac{2t}{1+t^2},\cos x=\frac{1-t^2}{1+t^2}$ thay vào PT ta thu được
$4t(t-1)(t+1) \left( {t}^{16}+{t}^{15}-6\,{t}^{14}-23\,{t}^{13}+80\,{t}^{12}+37\,{t}^{11}-250\,{t}^{10}+61\,{t}^{9}+606\,{t}^{8}-61\,{t}^{7}-250\,{t}^{6}-37\,{t}^{5}+80\,{t}^{4}+23\,{t}^{3}-6\,{t}^{2}-t+1 \right) =0$
PT bậc $16$ này vô nghiệm nên PT đã cho vô nghiệm.

Gọi $A(a,b) \in (S)$, $B(c, d) \in (d)$.
Mình làm trường hợp $OAB$ vuông cân tại $O$. Ta cần
$\begin{cases}A(a,b) \in (S)\\OA^2=OB^2 \\B(c, d) \in (d)\\ \overrightarrow{OA}.\overrightarrow{OB}=0 \end{cases}$
$\Leftrightarrow \begin{cases}a^2+b^2+a-7b=0 \\ a^2+b^2=c^2+d^2\\4c-3d+50=0 \\ac+bd=0\end{cases}$
Hệ này vô nghiệm nên không tìm được các điểm thỏa mãn bài toán.

Gọi $A(a,2-a) \in d_1$, $B(b,8-b) \in d_2$.
 Tam giác $MAB $ đều $\Leftrightarrow MA^2=MB^2=AB^2$
$\Leftrightarrow \begin{cases}(a-2)^2+a^2=(b-2)^2+(6-b)^2 \\ (a-2)^2+a^2=(a-b)^2+(a-b+6)^2\\(b-2)^2+(6-b)^2=(a-b)^2+(a-b+6)^2 \end{cases}$
Giải hệ này ta được
$a=1 \pm \frac{5}{\sqrt 3}$, $b=4 \pm \frac{4}{\sqrt 3}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Đặt
$x=\frac{a}{a+b}=\frac{1}{1+\frac{b}{a}}=\frac{1}{1+m}$
tương tự $y=\frac{1}{1+n}, z=\frac{1}{1+p}$.
Trong đó $mnp=1$ và $m,n,p>0.$
Ta cần tìm GTNN của
$x^2+y^2+z^2=\frac{1}{(1+m)^2}+\frac{1}{(1+n)^2}+\frac{1}{(1+p)^2}$
Trước hết bạn từ chứng minh BĐT sau coi như bài tập nhé
$\frac{1}{(1+m)^2}+\frac{1}{(1+n)^2} \ge \frac{1}{1+mn}$.
Vì nó tương đương với $mn(m-n)^2+(mn-1)^2 \ge 0$
Đẳng thức xảy ra khi $m=n=1$.
Như vậy ta có
$\frac{1}{(1+m)^2}+\frac{1}{(1+n)^2}+\frac{1}{(1+p)^2} \ge \frac{1}{1+mn}+\frac{1}{(1+p)^2}=\frac{p}{p+1}+\frac{1}{(1+p)^2}=\frac{p^2+p+1}{(1+p)^2}$
Viêc còn lại là đi chứng minh
$\frac{p^2+p+1}{(1+p)^2} \ge \frac{3}{4}\Leftrightarrow \frac{(p-1)^2}{4(p+1)^2} \ge 0$, luôn đúng.
Vậy GTNN cần tìm là $\frac{3}{4}\Leftrightarrow m=n=p=1\Leftrightarrow a=b=c=\frac{1}{2}$.

b)


Vậy Kết Quả là $C_5^3.C_5^3.6!-C_5^3.C_4^2.5!=64800$ số.

a)

b)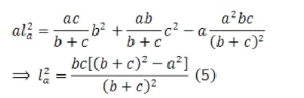

Điều này có nghĩa là
$AD=l_a=\frac{2}{b+c}\sqrt{bcp(p-a)}$ (đpcm)

a)