|
|
giải đáp
|
Giúp em nhé
|
|
|
|
a) Áp dụng BĐT tam giác ta có
$\begin{cases}\frac{2}{3}m_a+\frac{2}{3}m_b >c \\ \frac{2}{3}m_a+\frac{2}{3}m_c >b \\ \frac{2}{3}m_b+\frac{2}{3}m_c >a \end{cases}\Rightarrow \frac{3}{4} (a+b+c)<m_a+m_b+m_c$
Vẽ thêm điểm D để tạo ra hình bình hành ABCD và áp dụng BĐT tam giác ta có $2m_a<b+c$
$\Rightarrow \begin{cases}2m_a<b+c \\ 2m_b<a+c \\ 2m_c<b+a \\ \end{cases}\Rightarrow m_a+m_b+m_c<a+b+c$
|
|
|
|
giải đáp
|
Phương trình vô tỉ.
|
|
|
|
3. Điều kiện $x \ge -2$
$x^2+2x-2\sqrt{x+2}=4\Leftrightarrow x^2+2x-8-2(\sqrt{x+2}-2)=0$
$\Leftrightarrow (x+4)(x-2)-2(x-2)\frac{2}{\sqrt{x+2}+2}=0$
Do $x+4 \ge 2 >1\ge \frac{2}{\sqrt{x+2}+2}$.
Do vậy PT $\Leftrightarrow x=2.$
|
|
|
|
|
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
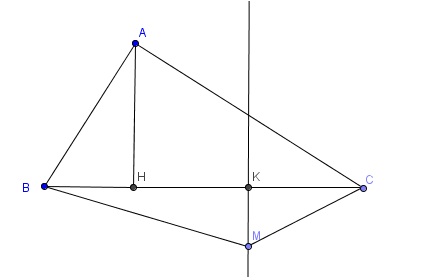 Áp dụng Định lý Py-ta-go ta được $MB^2-MC^2=(KB^2+KM^2)-(KC^2+KM^2)=KB^2-KC^2=(KB-KC)(KB+KC)$ $=(KB-KH)(KB+KC)=BH.BC=AB^2=\boxed{16 cm^2.}$ |
|
|
|
|
|
|
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
Trước hết bạn chứng minh bằng quy nạp hệ thức sau
$1+3+\cdots+(2n-1) = \sum_{k=1}^n(2k-1)=n^2$
Ta có $\mathop {\lim }\limits_{n \to \infty }(\frac{1+3+5+...+2n-1}{n+1}$-$\frac{2n+1}{2})=\mathop {\lim }\limits_{n \to \infty }(\frac{n^2}{n+1}-\frac{2n+1}{2})=\mathop {\lim }\limits_{n \to \infty }(\frac{n^2}{n+1}-\frac{2n+1}{2})$
$=\mathop {\lim }\limits_{n \to \infty }-\frac{3n+1}{2n+2}=-\frac{3}{2}$
|
|
|
|
giải đáp
|
mọi người giải giúp
|
|
|
|
Giả sử $\alpha=m+ni, z=x+yi$ trong đó $m,n$ là các số thực cho trước, $x,y$ là các số thực thay đổi.
Từ câu 1 ta có
$k=|m+x+(n+y)i|^2-(m^2+n^2)\Rightarrow (x+m)^2+(y+n)^2=k+m^2+n^2$
Nếu $k< -m^2-n^2$. Tập hợp các điểm $z$ là tập hợp rỗng.
Nếu $k= -m^2-n^2$. Tập hợp các điểm $z$ là điểm $-\alpha.$
Nếu $k> -m^2-n^2$. Tập hợp các điểm $z$ là đường tròn tâm $(-m;-n)$ bán kính $\sqrt{k+m^2+n^2}$.
|
|
|
|
giải đáp
|
mọi người giải giúp
|
|
|
|
1. Ta có
$z\overline{z} +\overline{\alpha}z+\alpha \overline{z}+\alpha \overline{\alpha}=z(\overline{\alpha}+\overline{z})+\alpha(\overline{\alpha}+\overline{z})=(z+\alpha)(\overline{\alpha}+\overline{z})=(z+\alpha)\overline{z+\alpha}=|z+\alpha|^2$.
Từ đây suy ra đpcm.
|
|
|
|
giải đáp
|
Tìm tiếp tuyến
|
|
|
|
Gọi $M(0;a )$, suy ra tiếp tuyến tại $M$ có dạng $y=kx+a$
Để từ $M$ kẻ được $3$ tiếp tuyến thì
$\begin{cases}x^4-2x^2= kx+a\\ 4x^3-4x=k \end{cases}$ có $3$ nghiệm phân biệt
Thay PT hai vào PT một ta có
$x^4-2x^2= (4x^3-4x)x+a\Leftrightarrow 3x^4-2x^2=-a$
Lập bảng biến thiên của $f(x)=3x^4-2x^2$ thì ta thấy $y=0$ là đường thẳng duy nhất cắt hàm số tại $3$ điểm phân biệt.
Vậy $a=0$ và $M(0;0).$
|
|
|
|
giải đáp
|
giải hệ phương trình sau giúp mình với
|
|
|
|
Nhận thấy $x=-1$ không phải là nghiệm của hệ. Từ PT thứ hai ta có $y=\frac{2x}{x+1}$.
Thay vào PT thứ nhất và thu gọn ta được
$2x^3+x^2-(\frac{2x}{x+1})^2-\frac{2x^2}{x+1}(x+\frac{2x}{x+1})=0$
$\iff x^2(x-1)(2x+3)=0$
Vậy $(x;y) \in \left\{ {(0;0), (1,1); (-3/2;6)} \right\}$
|
|
|
|
giải đáp
|
giúp em bài này nữa ạ
|
|
|
|
b) Trước hết giải hệ
$\begin{cases}3x+2y-10=0\\7x-2y-10=0\end{cases}\Leftrightarrow \begin{cases}x=2 \\ y=2 \end{cases}$
Để ba đường thẳng đồng quy thì $x=y=2$ phải thỏa mãn PT thứ ba, như vậy
$4m+6-7=0\Leftrightarrow m=1/4$
|
|
|
|
giải đáp
|
giúp em bài này nữa ạ
|
|
|
|
a)
$\begin{cases}(3+n)x-5y=-4\\5x-(4-m)y=5 \end{cases}$
Điều kiện bài toán $\Leftrightarrow \frac{3+n}{5}=\frac{-5}{-(4-m)}=\frac{-4}{5}\Leftrightarrow \begin{cases}m=\frac{41}{4} \\ n=-7 \end{cases}$
|
|