a)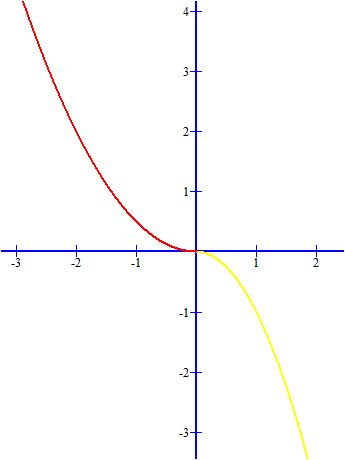

Đồ thị $y= \frac{1}{2}x^2$  khi $ -3\leq x\leq 0$ có màu đỏ trên hình vẽ
Đồ thị $y= -x^2$  khi $ 0\leq x\leq 2$ có màu vàng trên hình vẽ

Đặt $a=\sqrt[3]{3(1+\sqrt[3]{2}+\sqrt[3]{4})},   b=\sqrt{\frac{1}{4}+\sqrt[3]{2}+\sqrt[3]{4}}$
Ta có điều sau :
$\sqrt[3]{3(1+\sqrt[3]{2}+\sqrt[3]{4})}-\sqrt{\frac{1}{4}+\sqrt[3]{2}+\sqrt[3]{4}}=\frac{1}{2}$
Bạn có thể tự chứng minh coi như bài tập nhé.
PT $\Leftrightarrow \sqrt[3]{3x^2-3x+3}-a=\sqrt{\frac{x^3}{3}-\frac{3}{4}}-b$
$\Leftrightarrow \frac{3(x+\sqrt[3]{2})(x-\sqrt[3]{2}-1)}{A^2+Aa+a^2}=\frac{(x-\sqrt[3]{2}-1)f(x)}{B+b}         (*)$
Trong đó $A=\sqrt[3]{3x^2-3x+3},       B=\sqrt{\frac{x^3}{3}-\frac{3}{4}}$
Kiểm tra rằng từ $(*)$ PT đã cho chỉ có nghiệm duy nhất $x=\sqrt[3]{2}+1$
Nếu bạn đang học phổ thông thì không nên lo lắng vì bài tập này do tính chất nghiệm không đơn giản. Còn nếu bạn đã làm quen với một số phần mềm để có thể kiểm tra được nghiệm của PT thì trên đây là câu trả lời có thể chấp nhận được.

từ HPT $\Rightarrow 11(x^{2}+3xy+y^{2})=12(x^{2}-3xy+3y^{2})\Leftrightarrow x^2-69xy+25y^2=0\Leftrightarrow x=\frac{1}{2}\left ( 69 \pm\sqrt{4661} \right )y$
Thay điều này vào PT thứ nhất ta được
$x=\pm\frac{5}{2}\sqrt{1-\sqrt{\frac{7}{11}}}$ và $y=\frac{2x}{ 69 \pm\sqrt{4661}}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

b) $x^2-2x(m-2)=0\Leftrightarrow x(x-2m+4)=0\Leftrightarrow \left[ {\begin{matrix} x=0\\ x=2(m-2) \end{matrix}} \right.$
 Nhận thấy với mọi giá trị của $m$ thì PT đều có nghiệm $x=0$, không âm.
Nếu câu hỏi được thay đổi là tìm $m$ để PT có nghiệm dương thì điều kiện là $m>2.$

c) PT có hai nghiệm đều âm
$\Leftrightarrow \begin{cases}m \ne 0\\\Delta' \ge 0 \\ S=-\frac{b}{a}<0 \\ P=\frac{c}{a}>0\end{cases}\Leftrightarrow \begin{cases}m\ne 0 \\12m+1 \ge 0 \\ -\frac{2m+1}{m}<0 \\ \frac{m-2}{m}>0\end{cases} \Leftrightarrow m>2$

Các điểm được ký hiệu như trên hình vẽ. Và ta cần chứng minh giao điểm $M, N$ là các trung điểm của $AB,DC$.
Thật vậy theo định lý Talet
$\frac{AM}{DN}=\frac{SA}{SD}=\frac{AB}{CD}=\frac{AO}{CO}=\frac{AM}{CN}$
Tóm lại $\frac{AM}{DN}=\frac{AM}{CN} \implies DN=CN$ hay $N$ là trung điểm $CD$.
CHứng minh tương tự ta cũng có $M$ là trung điểm $AB$.

b) Thấy rằng $\sin\frac{\pi}{n} \ne 0$ và áp dụng công thức $2\sin a \sin b= \cos (a-b) -\cos (a+b)$
$\sum\limits_{i=1}^n 2\sin \frac{2(i-1)\pi}{n}\sin\frac{\pi}{n}=\sum\limits_{i=1}^n\left ( \cos \frac{(2i-3)\pi}{n}-\cos \frac{(2i-1)\pi}{n}\right )=$
$ \cos \frac{-\pi}{n}-\cos \frac{(2n-1)\pi}{n} =\cos \frac{\pi}{n}- \cos \left ( 2\pi-  \frac{\pi}{n}\right )=0$
Từ đây suy ra đpcm. 

a) Thấy rằng $\sin\frac{\pi}{n} \ne 0$ và áp dụng công thức $2\cos a \sin b= \sin (a+b) -\sin (a-b)$
$\sum\limits_{i=1}^n 2\cos \frac{2(i-1)\pi}{n}\sin\frac{\pi}{n}=\sum\limits_{i=1}^n\left ( \sin \frac{(2i-1)\pi}{n}-\sin \frac{(2i-3)\pi}{n}\right )=$
$ \sin \frac{(2n-1)\pi}{n}+ \sin \frac{\pi}{n}= \sin \left ( 2\pi-  \frac{\pi}{n}\right )+ \sin \frac{\pi}{n}=0$
Từ đây suy ra đpcm. 

b) $N=\cos(180^0-x)-2\sin(180^0-x)+\cos x+2\sin(90^0-x)=$
$-\cos x -2\sin x+\cos x+2\cos x=2\cos x- 2\sin x$

a) 
$M=\cos(90^0-x)+\sin(x+90^0)-\tan(180^0-x).\cot x=$
$\sin x+\sin(180^0-x-90^0)+\tan x.\cot x=$
$=\sin x+\sin(90^0-x)+1=\sin x+\cos x +1$ 

b) $\cos 2A+\cos 2B-\cos 2C- \frac{3}{2}=2\cos (A+B)\cos (A-B)+1-2\cos^2 C- \frac{3}{2}$
  $=-2\cos^2 C-2\cos C\cos (A-B)- \frac{1}{2} =-2\left[ {\cos^2 C+\cos C\cos (A-B)+ \frac{1}{4} \cos^2 (A-B)} \right]+\frac{1}{2} \cos^2 (A-B)- \frac{1}{2} $
$=-2\left ( \cos C+ \frac{1}{2}\cos (A-B) \right )^2+ \frac{1}{2}\left ( \cos^2 (A-B)-1 \right )\le 0$
 Từ đây suy ra đpcm.
 Đẳng thức xảy ra khi và chỉ khi tam giác $ABC$ đều.

a) $\cos 2A-\cos 2B+\cos 2C- \frac{3}{2}=2\cos (A+C)\cos (A-C)+1-2\cos^2 B- \frac{3}{2}$
 $=-2\cos^2 B-2\cos B\cos (A-C)- \frac{1}{2} =-2\left[ {\cos^2 B+\cos B\cos (A-C)+ \frac{1}{4} \cos^2 (A-C)} \right]+\frac{1}{2} \cos^2 (A-C)- \frac{1}{2} $
$=-2\left ( \cos B+ \frac{1}{2}\cos (A-C) \right )^2+ \frac{1}{2}\left ( \cos^2 (A-C)-1 \right )\le 0$
 Từ đây suy ra đpcm.
 Đẳng thức xảy ra khi và chỉ khi tam giác $ABC$ đều.

Điều kiện $x>0.$
       $\log _3 \frac{3}{x} .\log_2 x -\log _3 \frac{x^3}{\sqrt{3}} = \frac{1}{2} +\log _2 \sqrt{x}$
$\Leftrightarrow \left ( 1-\log_3 x \right ) .\log_2 x -\left (3\log_3 x-\log_3 3^\frac{1}{2} \right )= \frac{1}{2} + \frac{1}{2}\log _2 x$
$\Leftrightarrow \left ( 1-\log_3 x \right ) .\log_2 x -\left (3\log_3 x- \frac{1}{2} \right )= \frac{1}{2} + \frac{1}{2}\log _2 x$
$\Leftrightarrow \log_3 x .\log_2 x - \frac{1}{2}\log _2 x+3\log_3 x=0$
$\Leftrightarrow \frac{\ln x}{\ln 3} . \frac{\ln x}{\ln 2} - \frac{1}{2} \frac{\ln x}{\ln 2}+3 \frac{\ln x}{\ln 3}=0$
$\Leftrightarrow \frac{1}{\ln 3\ln 2}\ln^2 x+\ln x\left ( \frac{3}{\ln 3}-\frac{1}{2\ln 2}\right )=0$
PT này là PT bậc hai theo $\ln x$  có 2 nghiệm ,bạn tự giải tiếp nhé

b) Xét HPT sau
$\begin{cases}2x+3y-2z=m\\ 2x+y+3z=4 \\ 3x+4y-3z=6 \end{cases}$
Bằng phương pháp giải hệ ta có được kết quả
$\begin{cases}x=14-3m \\ y=3(m-4)\\z=m-4 \end{cases}$
Từ điều kiện $x,y,z \ge 0$ ta suy ra $4 \le m \le \frac{14}{3}$
Vậy
$\min 2x+3y-2z =4$ chẳng hạn khi $(x,y,z)=(2,0,0)$
$\max 2x+3y-2z =\frac{14}{3}$ chẳng hạn khi $(x,y,z)=(0,2,\frac{2}{3})$