d) $y=\sqrt{x+2+2 \sqrt{x+1}}+\sqrt{x+2-2 \sqrt{x+1} }=\sqrt{x+1}+1+|\sqrt{x+1}-1|$
 Nếu $x \ge 0\Rightarrow y=\sqrt{x+1}+1+\sqrt{x+1}-1=2\sqrt{x+1} \ge 2$
 Nếu $0 >x \ge -1\Rightarrow y=\sqrt{x+1}+1-\sqrt{x+1}+1=2$
 Vậy $\min y=2$ chẳng hạn khi $x=0$.
 Trong trường hợp này việc sử dụng thành thạo phương pháp xét khoảng giá trị là điều cần thiết :)

b)
Làm tương tự như các phần trên với phương pháp xét trên các khoảng
 $x \ge 1$, $-2 \le x <1$, $-4 \le x <-2,  x \le -4$ ta được $\min y =5$ chẳng hạn tại $x=-2$.
Đây cũng là lý do mình không dùng bđt mà bạn nêu trên vì không muốn lo lắng dấu bằng xảy ra :)

Kẻ $SO \perp (ABC)$. Từ giả thiết cạnh bên hợp với đáy các góc bằng nhau suy ra $O$ là tâm đường tròn ngoại tiếp $ABC$.
Theo công thức Heron thì diện tích tam giác $ABC$ là
$S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{4.1.1.2}=2\sqrt 2$
Từ đó
$R=AO=BO=CO=\frac{abc}{4S}=\frac{3.3.2}{8\sqrt 2}=\frac{9}{4\sqrt 2}$
$\Rightarrow SO=R.\tan \alpha=R.\sqrt{\frac{1}{\cos^2 \alpha}-1}=\frac{9}{4\sqrt 2}.3\sqrt2=\frac{27}{4}$
Như vậy $V_{SABC}=\frac{1}{3}.\frac{27}{4}.2\sqrt 2=\frac{9\sqrt 2}{2}$

d) Xét
$y^2=( 5|x|+2 \sqrt{2-3 x^2 }  )^2=25x^2+8-12x^2+20|x|\sqrt{2-3 x^2}=13x^2+8+20|x|\sqrt{2-3 x^2} \ge 8$
Vậy $\min y=2\sqrt2 \Leftrightarrow x=0$

c) Xét
$y^2=(3 x^2+\sqrt{1-x^4})^2=9x^4+1-x^4+6x^2\sqrt{1-x^4}=8x^4+1+6x^2\sqrt{1-x^4} \ge 1$
Vậy $\min y=1 \Leftrightarrow x=0$

b) Mình nghĩ là phần b) bạn viết thiếu đề bài vì nếu không chắc chắn BĐT không đúng với nhiều trường hợp. Mình đoán bạn muốn nhắc đến bài toán trong phần b) tại đây
http://toan.hoctainha.vn/Thu-Vien/Bai-Tap/104578/bai-104578

b) Xét
$y^2=(\sqrt{x^2+x+1}+\sqrt{x^2-x+1} )^2=x^2+x+1+x^2-x+1+2\sqrt{(x^2+x+1)(x^2-x+1)} =2x^2+2+2\sqrt{x^4+x^2+1}$
Sử dụng $x^4,x^2 \ge 0$ ta suy ra $y^2 \ge 4 \implies \min y=2 \iff x=0$

a) Xét $y^2=(\sqrt{2x-2}+\sqrt{3-2x} )^2=2x-2+3-2x+2\sqrt{2x-2}\sqrt{3-2x} =1+2\sqrt{2x-2}\sqrt{3-2x} \ge 1$
vậy $\min y=1\Leftrightarrow \sqrt{2x-2}\sqrt{3-2x}=0\Leftrightarrow x=1$ hoặc $x=3/2$

d) $\overrightarrow{AB}=\overrightarrow{DC}$
$\overrightarrow{AD}=\overrightarrow{BC}$

c) Các vecto ngược hướng
$\overrightarrow{AB}$ và $\overrightarrow{CD}$
$\overrightarrow{AD}$ và $ \overrightarrow{CB}$
$\overrightarrow{IA}$ và $ \overrightarrow{IC}$
$\overrightarrow{IB}$ và $ \overrightarrow{ID}$

b) Các vecto cùng hướng
$\overrightarrow{AB}$ và $ \overrightarrow{DC}$
$\overrightarrow{AC}$ và $ \overrightarrow{AI}$
$\overrightarrow{AD}$ và $ \overrightarrow{BC}$
$\overrightarrow{BD}$ và $ \overrightarrow{BI}$

a) Các vecto cùng phương
$\overrightarrow{AB}$ và $ \overrightarrow{DC}$
$\overrightarrow{AD}$ và $ \overrightarrow{BC}$
$\overrightarrow{AI}$ và $ \overrightarrow{AC}$
$\overrightarrow{BI}$ và $ \overrightarrow{BD}$

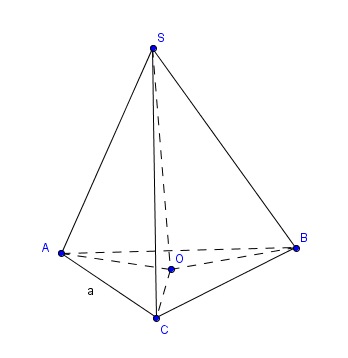Gọi $SO$ là đường cao của hình chóp thì $SO \perp (ABC)$ và $O \in mp(ABC).$
Do các cạnh bên tạo với đáy góc $45^\circ$ nên từ định nghĩa góc tạo bởi đường thẳng và mặt phẳng suy ra
$\widehat{SAO}=\widehat{SBO}=\widehat{SCO}=45^\circ$
Do đó $SAO, SBO, SCO$ là các tam giác vuông cân nên $AO=BO=CO$ vì đều bằng $SO.$
Từ đây suy ra $O$ là tâm đường tròn ngoại tiếp của tam giác vuông $ABC$ tại $C$ nên nó là trung điểm $BC$
Kéo theo $SO=AO=\frac{1}{2}BC$
Mặt khác tam giác vuông $ABC$ tại $C$ có $A=60^\circ$ nên $BC=\frac{AC}{\cos 60}=2a$
Theo định lý Pytago ta tính được $BC=\sqrt{AB^2-AC^2}=\sqrt{(2a)^2-a^2}=a\sqrt 3$
Vậy $V_{S.ABC}=\frac{1}{3}SO.S_{ABC}=\frac{1}{3}.\frac{1}{2}BC.\frac{1}{2}BC.AC=\frac{a^3\sqrt 3}{3}$ (đơn vị diện tích).

b) Nếu ở đề bài không có điều kiện $x, y>0$ thì ta phải dùng phương pháp hàm số.
$B=f(x)=x(1-x)^3\Rightarrow f'(x)=(x-1)^2(1-4x)$
Lập bảng biến thiên của hàm số này và ta được
$\max B = \max f(x)=\frac{27}{256}\Leftrightarrow \begin{cases}x=1/4 \\ y=3/4 \end{cases}$

c) Hiển nhiên thấy
$\frac{1}{ \sqrt{1}+ \sqrt{2}}+ \frac{1}{ \sqrt{2}+ \sqrt{3}}+...+\frac{1}{ \sqrt{11}+ \sqrt{12}}=\left ( \sqrt{2}- \sqrt{1} \right )+\left ( \sqrt{3}- \sqrt{2} \right )+...+\left ( \sqrt{12}- \sqrt{11} \right )= \sqrt{11}- 1 $
Mà $2< \sqrt{11}- 1 <3$ nên có đpcm.