|
|
|
|
|
|
|
|
|
|
|
|
|
|
đặt câu hỏi
|
tập hợp
|
|
|
|
G= { x$\epsilon$Q sao cho x= $\frac{1}{3^{n}}$ và n $\in$N, x $\geq$ $\frac{1}{18}$ }
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 30/05/2016
|
|
|
|
|
|
|
|
đặt câu hỏi
|
Hình học
|
|
|
|
Từ điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB và AC tới đường tròn (O; R), (B, C là hai tiếp điểm). Đường thẳng d tùy ý đi qua điểm A cắt đường tròn (O) tại hai điểm phân biệt P và Q sao cho tia AP nằm giữa hai tia AB và AO. Đường thẳng đi qua O và song song với d cắt đường thẳng AC tại điểm N. Gọi M là trung điểm của đoạn thẳng PQ.
1) Chứng minh các điểm A, B, M, O, C cùng nằm trên một đường tròn. 2) Chứng minh $\Delta $AON ~ $\Delta$MCO 3) Giả sử OA = 3√10 cm, R = 5cm và OM = 3 cm. Đặt $\widehat{AON}$= α, tính sin α, cos α, tg α và cotg α 4) Chứng minh 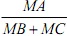 là đại lượng không đổi khi đường thẳng d quay quanh điểm A. là đại lượng không đổi khi đường thẳng d quay quanh điểm A.
Xem thêm : Mời mọi người tham gia cuộc thi do các Admin tổ chức nhé CLICK !
|
|
|
|
đặt câu hỏi
|
=))
|
|
|
|
1) Chứng minh rằng diện tích của những tứ giác có các đỉnh nằm trong hoặc trên một đường tròn bán kính R luôn nhỏ hơn hoặc bằng 2R$^{2}$
2) Cho x và y là các số thực dương thay đổi sao cho x + y = 2.
Tìm giá trị nhỏ nhất của A = $\frac{x^{2}+ 3y^2}{2xy^2 - x^2y^3}$ |
|
|
|
|
|
|
|
|
|
|
|