|
|
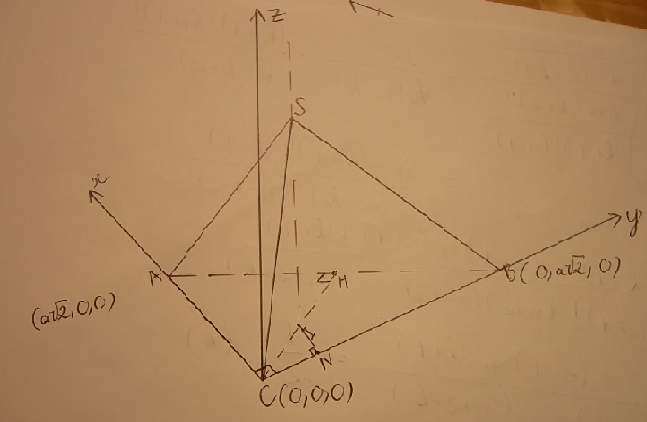
Gắn hệ trục tọa độ vào hình vẽ sao cho C trùng O (0,0,0), CA trùng Ox, CB trùng Oy. Từ C kẻ Cz song song SI => Cz vuông góc với mp (ABC)
Khi đó: C(0,0,0), A(a$\sqrt{2}$,0,0), B(0,a$\sqrt{2}$,0)
(Do $\Delta$ABC là tam giác vuông tại C => AB=AC$\sqrt{2}$ => AC= a$\sqrt{2}$)
$\Delta$ABC là tam giác vuông cân tại C, H là trung diểm AB => CH vuông góc với AB
Trong mp (ABC) , kẻ IN vuông góc với CB
Xét $\Delta$CNI đồng dạng $\Delta$CHB
=> $\frac{IN}{BH}$=$\frac{CI}{CB}$=> IN=$\frac{a}{2\sqrt{2}}$ (BH=1/2AB; CI=1/2CH=1/4AB=a/2)
I cách đều AB, AC=> IA=IB=> I($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,0)
=> S($\frac{a}{2\sqrt{2}}$,$\frac{a}{2\sqrt{2}}$,$\frac{a}{2}$)
Gọi G(x,y,z) là tâm mặt cầu S.ABI => GA=GB=GC=GS
Giải hệ 3 phương trình 3 ẩn được tọa độ G($\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4\sqrt{2}}$,$\frac{-3a}{4}$)
Từ đó, bán kính mặt cầu S.ABI là R=GA= $\frac{a\sqrt{13}}{2\sqrt{2}}$
|