Làm bài hình cho đỡ khô khan

Question

Cho hình nón đỉnh

$S$ đáy là hình tròn

$(O;R)$ . Một mặt phẳng

$(\alpha)$ vuông góc với

$SO$ tại điểm

$H$ thuộc đoạn

$SO$ và cắt hình nón theo đường tròn

$(C)$ . Đặt

$OH=x (0<x<h)$ Tìm

$x$ để thể tích hình nón đỉnh

$O$ đáy là hình tròn

$(C)$ đặt giá trị lớn nhất.

score 6 · Answer 1

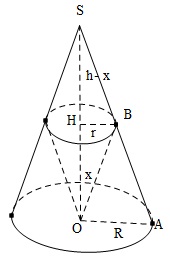
Gọi

$r$ là bán kính đáy của

$(C), V$ là thể tích hình nón đỉnh

$O$ đáy là hình tròn

$(C)$ , ta có:

$\frac{r}{R}=\frac{SH}{SO}=\frac{h-x}{h} \Rightarrow r=\frac{(h-x)R}{h}$

$\Rightarrow V=\frac{1}{3}\pi r^2.x=\frac{1}{3} \pi.\frac{R^2}{h^2}(h-x)^2 x=\frac{\pi R^2}{6h^2}(h-x)^2.2x$
Áp dụng bất đẳng thức Cô-si cho

$3$ số

$2x,h-x,h-x$ ta được

$2h=h-x+h-x+2x \geq 3\sqrt[3]{(h-x)^2.2x}$
Dấu "=" xảy ra khi

$x=\frac{h}{3}$
Khi đó

$V=\frac{\pi R^2}{6h^2}(h-x)^2 \leq \frac{\pi R^2}{6h^2}.\frac{8h^3}{27}=\frac{4\pi R^2h}{81}$
Vậy khi

$x=\frac{h}{3}$ thì thể tích

$V$ đạt giá trị lớn nhất (

$\max V=\frac{4\pi R^2h}{81}$ )

1 Đáp án