|
|
AC= $\sqrt{AB^{2}+BC^{2}}$= 2$\sqrt{5}$a
Xét $\Delta$SAC vuông tại A, tan SAC= $\frac{SA}{AC}$= $\frac{\sqrt{3}}{3}$ => SA= $\frac{2\sqrt{15}a}{3}$
Ghép hình với hệt rục tọa độ trong không gian, sao cho A trùng O, AB trùng Ox, AD trùng Oy, AS trùng Oz
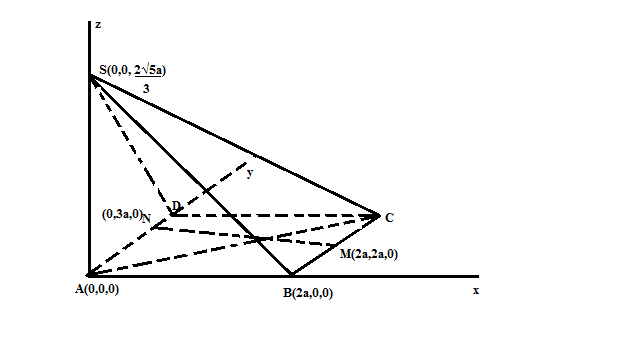
Khi đó tọa độ các điểm là: A(0,0,0), B(2a,0,0), M(2a,2a,0), N(0,3a,0), S( 0,0, $\frac{2\sqrt{5}a}{3}$)
Theo công thức tính khoảng cách 2 đường chéo nhau trong không gian thì: d( $\overrightarrow{SB}$, $\overrightarrow{MN}$)= $\frac{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right].\overrightarrow{MB}} \right|}{\left| {\left[ {\overrightarrow{SB},\overrightarrow{MN}} \right]} \right|}$= $\frac{4\sqrt{5}a}{\sqrt{34}}$
|