|
|
$1$.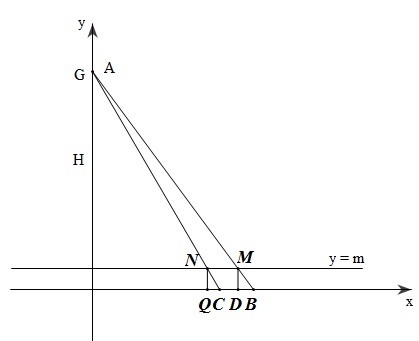
Từ giả thiết ta có \(H\left( {0,\,\,3} \right);\,\,E\left( {\frac{7}{2},\,\,0} \right)\)
Đường thẳng $AB$ có phương trình \(\frac{x}{4} + \frac{y}{6} = 1\)
Thế $y = m$ vào phương trình $AB$ \( \Rightarrow x = 4 - \frac{{2m}}{3}\)
Đường thẳng $AC$ có phương trình \(\frac{x}{3} + \frac{y}{6} = 1\)
Thế $y = m$ vào phương trình $AC$ \( \Rightarrow x = 3 - \frac{m}{2}\)
Do đó ta tìm được tọa độ \(M\left( {4 - \frac{{2m}}{3},\,\,m} \right);\,N\left( {3 - \frac{m}{2},\,\,m} \right)\) Tâm I của hình chữ nhật $MNPQ$ có tọa độ:
\(\left\{ \begin{array}{l}
x = \frac{{{x_M} + {x_N}}}{2} = \frac{7}{2} - \frac{{7m}}{{12}}\\
y = \frac{{{y_M} + {y_N}}}{2} = m
\end{array} \right.\)
Đường thẳng $HE$ có phương trình \(\frac{x}{{7/2}} + \frac{y}{3} = 1 \Leftrightarrow \frac{{2x}}{7} + \frac{y}{3} = 1\)
Tọa độ I thỏa mãn phương trình \(HE \Rightarrow I \in HE \Rightarrow H,\,E,\,I\) thẳng hàng
$2$. Gọi $O’$ là tâm đường tròn ngoại tiếp tam giác $ABC$ thì $O’$ nằm trên trung trực $BC$ \( \Rightarrow {X_{O'}} = \frac{7}{2}\). Gọi $y$ là tung độ của $O’$ thì tọa độ \(O'\left( {\frac{7}{2},\,y} \right)\), $O’$ là tâm đường tròn ngoại tiếp $ABC$
\( \Leftrightarrow O'A = O'B \Leftrightarrow {\left( {0 - \frac{7}{2}} \right)^2} + {\left( {6 - y} \right)^2} = {\left( {\frac{7}{2} - 4} \right)^2} + {\left( {y - 0} \right)^2} \Leftrightarrow y = 4\)
Vậy \(O'\left( {\frac{7}{2},\,4} \right)\) là tâm đường tròn $ABC$.
$3$. $T$ chính là giao điểm của đường thẳng $AC$ với đường tròn đường kính $OB$
$AC$ có phương trình \(\frac{x}{3} + \frac{y}{6} = 1 \Leftrightarrow y = 6 - 2x\left( 1 \right)\)
Đường tròn đường kính $OB$ có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 0} \right)^2} = 4\,\,\,\left( 2 \right)\)
Thế $(1)$ vào $(2)$ \( \Rightarrow {\left( {x - 2} \right)^2} + {\left( {6 - 2x} \right)^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \frac{{18}}{5}\end{array} \right.\)
Thế trở lại $(1)$ \( \Rightarrow \left[ \begin{array}{l}
y=6 - 2.2 = 2\\
y = 6 - \frac{{36}}{5} = \frac{{ - 6}}{5}
\end{array} \right.\)
Vậy trên đường thẳng $AC$ có hai điểm thỏa mãn bài ra là \({T_1}\left( {2,\,2} \right);\,\,{T_2}\left( {\frac{{18}}{5},\,\,\frac{{ - 6}}{5}} \right)\).
|
|
|
Đăng bài 27-04-12 11:26 AM
|
|