|
|
1. Khái niệm cực trị của hàm số
ĐỊNH NGHĨA
Giả sử hàm số f xác định trên tập hợp (D) ($D \in R$) và ${x_0} \in D$
a) ${x_0}$ được gọi là một điểm cực đại của hàm số f nếu tồn tại một khoảng (a; b) Chứa điểm${x_0}$ sao cho$(a;b) \subset D$
$f(x) < f({x_0})$với mọi $x \in (a;b)\backslash \left\{ {{x_0}} \right\}$
Khi đó$f({x_0})$được gọi là giá trị cực đại của hàm số f.
b) ${x_0}$ được gọi là một điểm cực tiểu của hàm số f nếu tồn tại một khoảng (a ; b) chứa điiểm ${x_0}$ sao cho$(a;b) \subset D$và
$f(x) > f({x_0})$với mọi $x \in (a;b)\backslash \left\{ {{x_0}} \right\}$
Khi đó$f({x_0})$ được gọi là giá trị cực tiểu của hàm số f
Điểm cực đại và cực tiểu được gọi chung là điểm cực tri.
Giá trị cực đại và cực tiểu được gọi chung là cực trị
CHÚ Ý
1) Giá trị cực đại (cực tiểu ) $f({x_0})$ của hàm số f nói chung không phải là giá trị lớn nhất (nhỏ nhất) của hàm số f trên tập hợp (D); $f({x_0})$chỉ là giá trị lớn nhất ( nhỏ nhất) của hàm số f trên một khoảng (a; b) nào đó chứa điểm ${x_0}$.
2) Hàm số f có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp (D).Hàm số cũng có thể không có cực tri trên một tập hợp số thực cho trước
3) Đôi khi người ta nói đến điểm cực trị của đồ thị
Nếu ${x_0}$ là một điểm cực trị của hàm số f thì điểm $({x_0};f({x_0}))$ được gọi là điểm cực trị của đồ thị hàm số f.
2. Điều kiên cần và đủ để hàm số đạt cực trị
ĐỊNH LÍ 1
Giả sử hàm số f đạt cực trị tại điểm ${x_0}$ khi đó , nếu f có đạo hàm tại ${x_0}$thì$f'({x_0}) = 0$
Điều ngược lại có thể không đúng
CHÚ Ý
Hàm số có thể đạt cưc trị tại một điểm mà tại đó hàm số không có đạo hàm chẳng hạn , hàm số $y = f(x) = \left| x \right|$ xác định trên . Vì $f(0) = 0$ và $f(x) > 0$với mọi $x \ne 0$ nên hàm số đạt cực tiểu tại điểm x = 0.
Dễ thấy hàm số $y = \left| x \right|$không có đạo hàm tại điểm x = 0
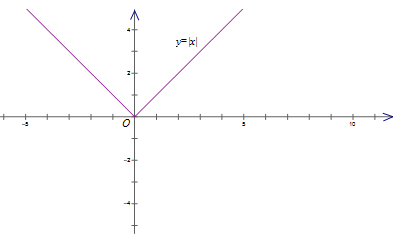
Như vậy, một hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.
3. Điều kiện đủ để hàm số đạt cực trị
ĐỊNH LÍ 2
Gỉả sử hàm số f liên tục trên khoảng ( a ;b ) chứa điểm ${x_0}$ Và có đạo hàm trên khoảng $(a;{x_0})\& ({x_0};b)$. Khi đó
a) Nếu$f'(x) < 0$ với mọi$x \in (a;{x_0})$và$f'(x) > 0$ với mọi$x \in ({x_0};b)$ thì hàm số f đạt cực tiểu tại điểm ${x_0}$.
b) Nếu $f'(x) > 0$với mọi $x \in (a;{x_0})$và $f'(x) < 0$với mọi $x \in ({x_0};b)$thì hàm số f đạt cực đại tại điểm${x_0}$.
Nói một cách khác
a, Nếu $f'(x)$đổi dấu từ âm sang dương khi x qua điểm ${x_0}$(theo chiều tăng) thì hàm số đạt cực tiểu tại điểm ${x_0}$.
b, Nếu$f'(x)$đổi dấu từ dương sang âm khi x qua điểm ${x_0}$(theo chiều tăng) thì hàm số đạt cực đại tại điểm ${x_0}$.
QUY TẮC
1)tìm$f'(x)$
2)tìm các điểm ${x_i}(i = 1,2,..)$tại đó đạo hàm của hàm số bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
3) Xét dấu $f'(x)$. Nếu $f'(x)$ đổi dấu khi x qua điểm ${x_i}$ thì hàm số đạt cực trị tại ${x_i}$.
ĐỊNH LÍ 3
Gỉa sử hàm số f có đạo hàm cấp 1 trên khoảng ( a ; b ) chứa điểm ${x_0}$ ; $f'({x_0}) = 0$và f có đạo hàm cấp hai khác 0 tại điểm ${x_0}$.
a) Nếu$f''({x_0}) < 0$ thì hàm số f đạt cực đại tại điểm ${x_0}$.
b) Nếu $f''({x_0}) > 0$thì hàm số f đạt cực tiểu tại điểm${x_0}$
QUY TĂC 2
1)Tìm $f'(x)$
2)Tìm các nghiệm${x_i}(i = 1,2,..)$.của phương trình $f'(x) = 0$
3)Tìm$f''(x)$và tính$f''({x_i})$
Nếu$f''({x_i}) < 0$thì hàm số đạt cực đại tại điểm ${x_i}$
Nếu $f''({x_i}) > 0$thì hàm số đạt cực tiểu tại điểm ${x_i}$
|