|
|
1 Định nghĩa tổng của hai vectơ
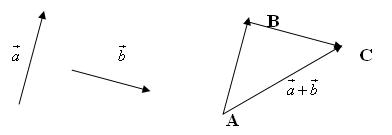
Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho khi đó vectơ$\overrightarrow {AC} $ được gọi là TỔNG của hai vectơ$\overrightarrow a $ và $\overrightarrow b $. Kí hiệu: $\overrightarrow {AC} = \overrightarrow a + \overrightarrow b $
Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ
2. Các tính chất của phép cộng vectơ
1.1 Tính chất giao hoán: $\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a $
1.2 Tính chất kết hợp: $\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)$
1.3 Tính chất của vectơ-không: $\overrightarrow a + \overrightarrow 0 = \overrightarrow a $
CHÚ Ý:
Do tính chất 2 , các vectơ$\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c \,\,\,\,va\,\,\,\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)$ bằng nhau, bởi vậy, từ nay chúng được viết một cách đơn giản là , và gọi là tổng của ba vectơ .
3. Các quy tắc cần nhớ
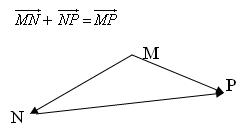
QUY TẮC BA ĐIỂM :
- Với ba điểm bất kì $M , N , P$ ta có
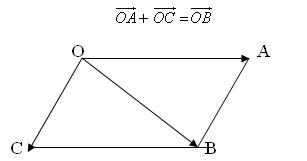
QUY TẮC HÌNH BÌNH HÀNH
-Nếu $OABC$ là hình bình hành ta có
Bài toán 2: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của vectơ tổng
Giải
Ta lấy điểm D sao cho ABCD là hình bình hành. Theo quy tắc hình bình hành ta có
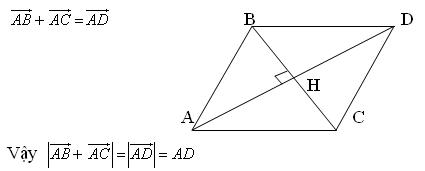
Vì $ABC$ là tam giác đều nên $ABCD$ là hình thoi và độ dài $AD$ bằng hai lần đường cao $AH$ của tam giác $ABC$, do đó $AD = 2 \times \frac{{a\sqrt 3 }}{2} = a\sqrt 3 $
Tóm lại, $\left| {\overrightarrow {AB} + \,\,\overrightarrow {AC} } \right| = a\sqrt 3 $
GHI NHỚ
- Nếu $M$ là trung điểm đoạn thẳng $AB$ thì
- Nếu $G$ là trọng tâm tam giác $ABC$ thì
CHÚ Ý :
- Quy tắc hình bình hành thường $\overrightarrow b $được áp dụng trong vật lí để xác định hợp lực của hai lực $\overrightarrow a $cùng tác dụng lên một vật
|