|
|
1. Định nghĩa mặt trụ:
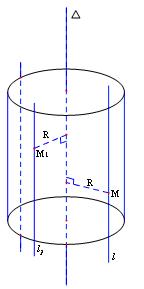
- Cho đường thẳng $\Delta $. Xét 1 đường thẳng l song song với $\Delta $, cách $\Delta $ một khoảng R.Khi đó: Mặt tròn xoay sinh bởi đường thẳng l như thế được gọi là mặt trụ tròn xoay hoặc đơn giản là mặt trụ
$\Delta $ gọi là trục của mặt trụ ,l gọi là đường sinh và R gọi là bán kính mặt trụ.Dễ thấy:
- Mặt trụ nói trên là tập hợp tất cả các điểm M cách đường thẳng $\Delta $ một khoảng cố định R không đổi
- Nếu ${M_1} $ là 1 điểm bất kỳ nằm trên mặt trụ thì đường thẳng ${l_1} $ đi qua ${M_1} $ và song song với $\Delta $ sẽ nằm trên mặt trụ đó. Như vậy đường thẳng ${l_1} $ cũng là đường sinh của mặt trụ
2. Hình trụ và khối trụ
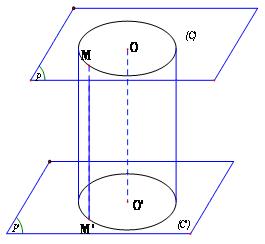
Cắt mặt trụ (T) trục $\Delta $, bán kính R bởi 2 mặt phẳng phân biệt (P) và (P’) cùng vuông góc với $\Delta $ ta được giao tuyến là 2 đường tròn (C) và (C’).
Ta có: Phần mặt trụ (T) nằm giữa 2 mặt phẳng (P) và (P’) cùng với 2 hình tròn xác định bởi (C) và (C’) được gọi là hình trụ
- Hai đường tròn (C) và (C’) được gọi là 2 đường tròn đáy, 2 hình tròn xác định bởi chúng được gọi là 2 mặt đáy của hình trụ, bán kính của chúng gọi là bán kính hình trụ. Khoảng cách giữa 2 mặt đáy gọi là chiều cao của hình trụ
- Nếu gọi O và O’ là tâm 2 hình tròn đáy thì đoạn OO’ gọi là trục của hình trụ
- Phần mặt trụ nằm giữa 2 đáy gọi là mặt xung quanh của hình trụ
- Với mỗi điểm M thuộc (C), có 1 điểm M’ thuộc (C’) sao cho MM’// OO’. Các đoạn thẳng như vậy gọi là đường sinh của hình trụ.
- Hình trụ cùng với phần bên trong của nó gọi là khối trụ
Ví dụ: Cho hình trụ có bán kính R và chiều cao cũng bằng R. Một hình vuông ABCD có 2 cạnh AB và CD lần lượt là dây cung của 2 đường tròn đáy, các cạnh AD và BC không phải đường sinh của hình trụ. Tính các cạnh hình vuông đó.
Giải:
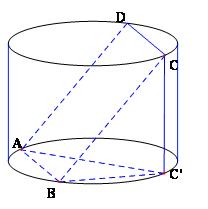
Gọi C’ là hình chiếu của C trên mặt đáy chứa AB thì $AB \bot BC' $ ( vì $AB \bot BC $). Vậy AC’ là đường kính của đường tròn đáy hay AC’ = 2R.
Từ các tam giác vuông ABC’ và CBC’ ta có:
$\begin{gathered}
BC{'^2} = AC{'^2} - A{B^2} = 4{R^2} - A{B^2} \\
BC{'^2} = B{C^2} - CC{'^2} = A{B^2} - {R^2} \\
\end{gathered} $
Suy ra $2A{B^2} = 5{R^2} \Leftrightarrow AB = \frac{{R\sqrt {10} }}{2} $
3. Diện tích hình trụ và thể tích khối trụ
- Định nghĩa:
Diện tích xung quanh của hình trụ là giới hạn của diện tích xung quanh của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn
Thể tích của khối trụ ( thể tích hình trụ ) là giới hạn của thể tích của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn
- Diện tích xung quanh của hình trụ bằng chu vi đáy nhân chiều cao
Thể tích của khối trụ bằng diện tích đáy nhân với chiều cao
Ví dụ: Cho hình trụ (T) có bán kính R, trục OO’ bằng 2R và mặt cầu (S) có đường kính OO’
a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ
b) Hãy so sánh diện tích mặt cầu và diện tích toàn phần của hình trụ
c) Hãy co sánh thể tích khối trụ (T) và mặt cầu (S)
Giải:
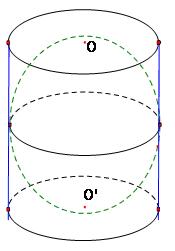
a) Dễ thấy rằng diện tích của mặt cầu và diện tích xung quanh hình trụ bằng nhau và bằng $4\pi {R^2} $
b) Diện tích toàn phần hình trụ bằng: $4\pi {R^2} + 2\pi {R^2} = 6\pi {R^2} $
Vậy diện tích mặt cầu bằng $\frac{2}{3} $ diện tích toàn phần hình trụ
c) Thể tích khối cầu: ${V_{(S)}} = \frac{4}{3}\pi {R^3} $
Thể tích khối trụ: ${V_{(T)}} = \pi {R^2}.2R = 2\pi {R^3} $
Vậy thể tích khối cầu bằng $\frac{2}{3} $ thể tích khối trụ
Normal
0
false
false
false
MicrosoftInternetExplorer4
|