|
|
1. Định nghĩa mặt nón: Cho đường thằng $\Delta $. Xét 1 đường thẳng l cắt $\Delta $ tại O và không vuông góc với $\Delta $
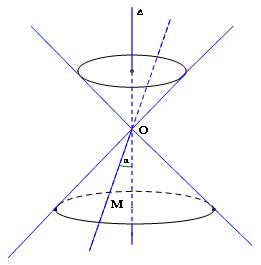
Mặt tròn xoay sinh bởi đường thẳng l như thế khi quay quanh $\Delta $ gọi là mặt nón tròn xoay hay đơn giản là mặt nón
- $\Delta $ gọi là trục của mặt nón
- l gọi là đường sinh của mặt nón
- O gọi là đỉnh mặt nón
- Nếu gọi $\alpha $ là góc giưa l và $\Delta $ thì $2\alpha $ gọi là góc ở đỉnh của mặt nón ( $0 < 2\alpha < {180^0} $)
2. Hình nón và khối nón
- Cho mặt nón $\Omega $ với trục $\Delta $, đỉnh O và góc ở đỉnh $2\alpha $. Gọi (P) là mặt phẳng vuông góc với $\Delta $ tại I khác O (HV51). Mặt phẳng (P) cắt mặt nón theo đường tròn (C) có tâm I. Gọi (P’) là mặt phẳng vuông góc với $\Delta $ tại O. Khi đó
Phần của mặt nón $\Omega $ giới hạn bởi 2 mặt phẳng (P) và (P’) cùng với hình tròn xác định bởi (C) gọi là hình nón
- Điểm O gọi là đỉnh hình nón, đường tròn (C) gọi là đường tròn đáy, hình tròn xác định bởi (C) gọi là đáy hình nón. Với mỗi điểm M nằm trên (C), đoạn OM gọi là đường sinh của hình nón. Đoạn OI gọi là trục hình nón, độ dài OI gọi là chiều cao hình nón
3. Khái niệm về diện tích hình nón và thể tích khối nón
- Một hình chóp gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón
- Ta có định nghĩa:
Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng vô hạn
Thể tích của khối nón là giới hạn của thể tích của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn
- Diện tích xung quanh của hình nón bằng 1 nửa tích số của độ dài đường tròn đáy và độ dài đường sinh
- Thể tích khối nón bằng một phần ba tích số diện tích hình tròn đáy và chiều cao
|