|
|
1. Hệ thức lượng trong tam giác vuông:
Cho ΔABC vuông ở A,AH là đường cao:
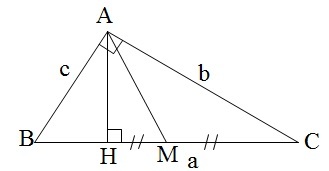
Ta có:
BC2=AB2+AC2 (định lí Pitago)
BA2=BH.BC
CA2=CH.CB
AB.AC=BC.AH
1AH2=1AB2+1AC2
BC=2AM. Với AM là đường trung tuyến của cạnh BC
sinB=ba,cosB=ca,tanB=bc,cotB=cb
b=a.sinB=a.cosC,c=a.sinC=a.cosB,
a=bsinB=bcosC,b=c.tanB=c.cotC
2. Hệ thức lượng trong tam giác thường:
* Định lí hàm số cosin
a2=b2+c2−2bc.cosA
* Định lí hàm số sin:
asinA=bsinB=csinC=2R
3. Các công thức tính diện tích.
a. Công thức tính diện tích tam giác:
S=12a.ha=12a.b.sinC=abc4R
=p.r=√p(p−a)(p−b)(p−c) (p=a+b+c2 là nửa chu vi tam giác)
Đặc biệt:
* ΔABC vuông ở A: S=12AB.AC
* ΔABC đều cạnh a: S=a2√34
b. Diện tích hình vuông: S= cạnh × cạnh
c. Diện tích hình chữ nhật: S= dài × rộng.
d. Diện tích tứ giác có hai đường chéo vuông góc:
S=12( chéo dài × chéo ngắn ).
e. Diện tích hình thang:
S=12( đáy lớn + đáy nhỏ )× chiều cao
g. Diện tích hình tròn: S=π.R2
|