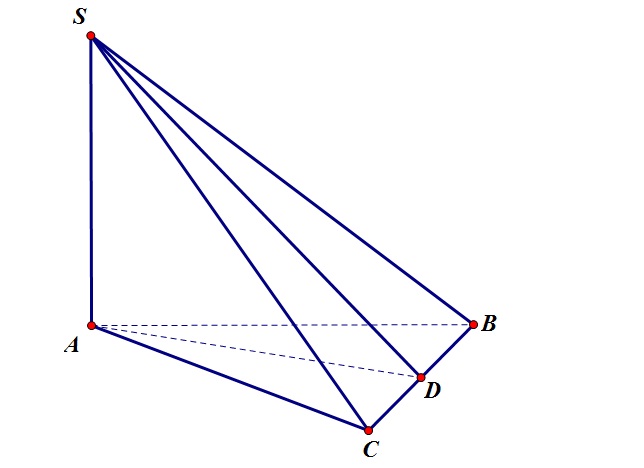
Theo giả thiết: $\angle SBA=\alpha$ .
Ta có: $AC=AB\Rightarrow SB=SC \Rightarrow SD\perp BC$
Mà $AD\perp BC \Rightarrow BC\perp(SAD) \Rightarrow \angle BSD=\beta$.
Ta có: $AB=SB.\cos\alpha, BD=SB.\sin\beta$
$\Rightarrow a^2=AD^2=SB^2(\cos^2\alpha-\sin^2\beta) \Rightarrow SB=\frac{a}{\sqrt{ \cos^2\alpha-\sin^2\beta }}$
Suy ra: $BD=SB\sin\beta= \frac{a\sin\beta}{\sqrt{ \cos^2\alpha-\sin^2\beta }} $
$SA=SB\sin\alpha= \frac{a\sin\beta}{\sqrt{ \cos^2\alpha-\sin^2\beta }} $
Từ đó: $V_{S.ABC}= \frac{a^3\sin\alpha\sin\beta}{3(\cos^2\alpha-\sin^2\beta)} $