2. 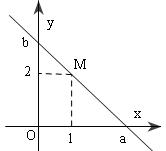
Vì $d$ cắt $(Ox), (Oy)$ nên phương trình $d$ có dạng : $\frac{x}{a} +\frac{y}{b} =1$
$d$ qua $M(1,2) : \frac{1}{a}+\frac{2}{b} =1 (*)$
Trường hợp một : $a=b\neq 0$
$(*)\Rightarrow \frac{1}{b}+\frac{2}{b}=1\Leftrightarrow b=3=a $
$\Rightarrow d : \frac{x}{3}+\frac{y}{3}=1 $ hay $x+y-3=0$
Trường hợp hai : $a=-b\neq 0$
$(*)\Rightarrow \frac{1}{-b}+\frac{2}{b}=1\Rightarrow b=1; a=-1 $
$\Rightarrow d : \frac{x}{-1}+\frac{y}{1}=1 $ hay $x-y+1=0$
Trường hợp $3: d$ qua $O(0,0),M(1,2)$
$d\equiv OM : \frac{y-y}{y_M-y_0}=\frac{x-x_0}{x_M-x_0} $
$\Rightarrow d : \frac{y}{2} =\frac{x}{1} $ hay $y=2x$ hay $2x-y=0$