|
|
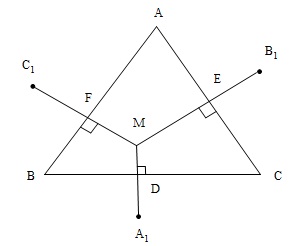
Gọi $D, E, F$ là giao điểm của $M{A_1},M{B_1},M{C_1}$ với các cạnh $BC,CA,AB$; $O$ là trọng tâm $\Delta ABC$. Ta có :
$\begin{array}{l}
\overrightarrow {M{A_1}} + \overrightarrow {M{B_1}} + \overrightarrow {M{C_1}} \\
= 2\left( {\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} } \right)\\
= 2.\frac{3}{2}\overrightarrow {MO} \,\,\,\,(*)\\
= 3\overrightarrow {MO}
\end{array}$
Điều này chứng tỏ $O$ cũng là trọng tâm của $\Delta {A_1}{B_1}{C_1}$
Chứng minh (*):
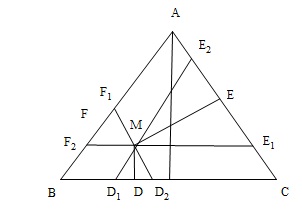
Qua $M$ kể các đường thẳng song song với các cạnh của tam giác $ABC$,
chúng chia tam giác $ABC$ thành các tam giác đều
${M_1}{D_1}{D_2};M{E_1}{E_2};M{F_1}{F_2}$ và các hình bình hành
$M{F_1}A{E_2};M{E_1}C{D_2};M{D_1}B{F_2}$
Ta có : $\left\{ \begin{array}{l}
\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{D_1}} + {{\overrightarrow {MD} }_2}} \right)\\
\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{E_1}} + \overrightarrow {M{E_2}} } \right)\\
\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{F_1}} + \overrightarrow {M{F_2}} } \right)
\end{array} \right.$
Cộng từng vế $3$ đẳng thức ta được
$\begin{array}{l}
\overrightarrow
{MD} + \overrightarrow {ME} + \overrightarrow {MF} =
\frac{1}{2}\left( {\overrightarrow {M{F_1}} + \overrightarrow {M{E_2}} }
\right) + \frac{1}{2}\left( {\overrightarrow {M{D_1}} +
\overrightarrow {M{F_2}} } \right) + \frac{1}{2}\left( {\overrightarrow
{M{E_1}} + \overrightarrow {M{D_2}} } \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
= \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} +
\overrightarrow {MC} } \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}3\overrightarrow {MO} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
= \frac{3}{2}\overrightarrow {MO\,}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\end{array}$
|
|
|
Đăng bài 04-05-12 08:53 AM
|
|