|
|
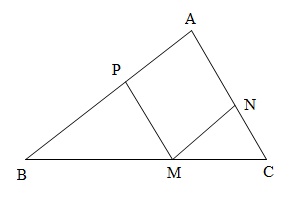
Dễ thấy $APMN$ là hình bình hành
$\begin{array}{l}
\Rightarrow \overrightarrow {PA} = \overrightarrow {MN} \\
\Rightarrow \left( {{x_A} - 5;{y_A} - 7} \right) = \left( {2; - 7} \right)\\
\Rightarrow \left\{ \begin{array}{l}
{x_A} - 5 = 2\\
{y_A} - 7 = - 7
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
{x_A} = 7\\
{y_A} = 0
\end{array} \right.\\
\Rightarrow A\left( {7;0} \right)
\end{array}$
Tương tự như vậy : $B\left( {3;14} \right),C\left( { - 1; - 10} \right)$
- Như ta đã biết, $G$ là trong tâm tam giác $ABC$ nên:
$\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3}\left( {7 + 3 - 1;0 + 14 - 10} \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3}\left( {9;4} \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \left( {3;\frac{4}{3}} \right)
\end{array}$
Vậy $G\left( {3;\frac{4}{3}} \right)$
|
|
|
Đăng bài 04-05-12 03:18 PM
|
|