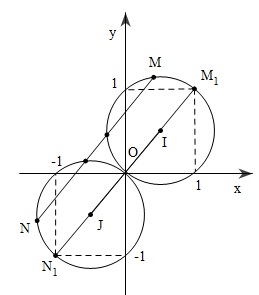
Trong mặt phẳng $Oxy$
$(1)\Leftrightarrow (a-\frac12)^2+(b-\frac12)^2=\frac12 \Rightarrow $ Đây là đường tròn tâm $I(\frac12;\frac12)$, bán kính: $\frac1{\sqrt 2} $
$(2) \Leftrightarrow (c+\frac{1}{2})^{2}+(d+\frac{1}{2})^{2}=\frac{1}{2}$
Đây là đường tròn tâm $J(-\frac{1}{2},-\frac{1}{2})$,bán kính $\frac{1}{\sqrt{2}}$
Xét $M(a,b),N(c,d)$
Lúc đó: $M_{1}N_{1}=M_{1}O+ON_{1}=\sqrt{2}+\sqrt{2}=2\sqrt{2}$
Và: $MN\le MO+NO=M_{1}N_{1}$
Dấu "=" xảy ra $\Leftrightarrow M\equiv M_1; N\equiv N_1$
$\Leftrightarrow a=b=1;c=d=-1$
Vậy: $\sqrt{(a-c)^{2}+(b-d)^{2}}\leq 2\sqrt{2} \Leftrightarrow (a-c)^{2}+(b-d)^{2}\leq 8$
$\Rightarrow$ (ĐPCM)