Bài 107375

Question

Cho

$a,b$ thỏa mãn:

$a-2b+2=0$ .Chứng minh rằng:

$\sqrt{a^{2}+b^{2}-6a-10b+34}+\sqrt{a^{2}+b^{2}-10a-14b+74}\geq 6 (1)$

score 0 · Answer 1

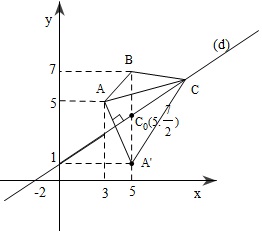
Xét trong mặt phẳng

$Oxy$ :

$(1)\Leftrightarrow \sqrt{(a-3)^{2}+(b-5)^{2}}+\sqrt{(a-5)^{2}+(b-7)^{2}}\geq 6$

Xét đường thẳng

$(d):x-2y+2=0$

$A(3,5);B(5,7)$

$C(a,b)\in (d)$ (vì:

$a-2b+2=0$ )

Suy ra:

$CA=\sqrt{(a-3)^{2}+(b-5)^{2}};CB=\sqrt{(a-5)^{2}+(b-7)^{2}}$

Gọi

$A'$ là điểm đối xứng của

$A$ qua

$(d)$
Gọi

$H(x,y)$ là hình chiếu của

$A$ lên

$d$
Ta có:

$\left\{ \begin{array}{l} H\in d\\ AH\bot d \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x-2y+2=0\\ 2(x-3)+(y-5)=0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x=4\\ y=3 \end{array} \right.$
Lại có:

$H$ là trung điểm

$A'A$
Suy ra: tọa độ

$A'(5,1)$

$A'B=\sqrt{(5-5)^{2}+(7-1)^{2}}=6$

Ta có:

$CA+CB=CA'+CB\geq A'B=6$

Dấu "=" xảy ra

$\Leftrightarrow C\equiv C_{0}$ (với

$C_0=BA'\cap d\Rightarrow C_0(5;\frac72) )$

$\Rightarrow \sqrt{(a-3)^{2}+(b-5)^{2}}+\sqrt{(a-5)^{2}+(b-7)^{2}}\geq 6$

Dấu "=" xảy ra

$\Leftrightarrow \begin{cases}a=5\\ b=\frac{7}{2} \end{cases}$

Bài 107375

1 Đáp án

Lý thuyết liên quan

Bài 107375

1 Đáp án

Liên quan

Lý thuyết liên quan