Bài 107158

Question

Cho hình lập phương

$ABCD.A'B'C'D'$ cạnh bằng

$2$ . Gọi

$M,N$ là trung điểm của

$AB, DD'$

a) Chứng minh

$MN//(BDC')$ . Tính

$MN$ và

$d(MN,(BDC'))$

b) Gọi

$P$ là trung điểm của

$C'D'$ . Tính

$V_{C.MNP}$ và góc giữa

$MN$ và

$BD$

c) Tính bán kính

$R$ của đường tròn

$(A'BD)$

hoàng anh thọ · Answer 1 · 6/7/2012 9:53:13 AM

Chọn hệ trục tọa độ

$Axyz$ sao cho:

$A(0;0;0),B(2;0;0), C(2;2;0), D(0;2;0), A'(0;0;2), B'(2;0;2), C'(2;2;2), D'(0;2;2)$

$\Rightarrow M(1;0;0), N(0;2;1), P(1;2;2)$

a) Ta có:

$\left\{ \begin{array}{l} \overrightarrow{MN}=(-1;2;1) \\ \overrightarrow{BD}=(-2;2;0) \\\overrightarrow{BC'}=(0;2;2) \end{array} \right.$

$\Rightarrow \overrightarrow{n}_{(BDC')}=[\overrightarrow{BD},\overrightarrow{BC'} ]=(4;4;-4)$

$\Rightarrow \overrightarrow{MN}.\overrightarrow{n}_{(BDC')}=0$

$\overrightarrow {MN} // (BDC')$ (do

$M\notin (BDC')$ )

Ta có

$MN=\sqrt{1+4+1}=\sqrt{6}$

$d(MN,(BDC'))=d(M,(BDC'))$ (do

$MN//(BDC')$ )

Phương trình

$(BDC'):x+y-z=0\Rightarrow d(MN,(BDC'))=\frac{|1-2|}{\sqrt{3} }=\frac{\sqrt{3} }{3}$

b) Ta có:

$V_{C.MNP}=\frac{1}{6}|[\overrightarrow{MN},\overrightarrow{MP} ].\overrightarrow{MC} |$

$=\frac{1}{6}|[(-1;2;1),(0;2;2)](1;2;0)| =1$ (đvtt)

$cos \varphi=\frac{|\overrightarrow{MN}.\overrightarrow{BD} |}{MN.BD} =\frac{|(-1;2;1)(-2;2;0)|}{\sqrt{6}.\sqrt{8} }=\frac{\sqrt{3} }{2}$

Vậy

$\varphi=30^0$

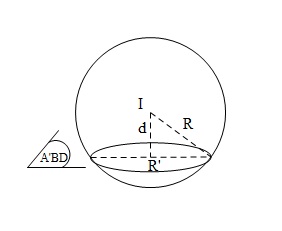
c) Gọi

$I, R'$ là tâm và bán kính của mặt cầu

$(S)$ ngoại tiếp hình lập phương

$\Rightarrow I$ là trung điểm của

$AC'$ và

$R'=\frac{AC'}{2} \Rightarrow I(1;1;1), R'=\sqrt{3}$

Phương trình

$(A'BD): \frac{x}{2}+\frac{y}{2}+\frac{z}{2}=1 \Leftrightarrow x+y+z-2=0$

$d=d(I,(A'BD))=\frac{\sqrt{3} }{3}$

Ta có:

$A', B, D \in (S)$

$\Rightarrow$ Đường tròn

$(A'BD)=(A'BD)\cap(S)$

$R=\sqrt{R^2-d^2}=\sqrt{3-\frac{1}{3} }=\frac{2\sqrt{6} }{3}$

Vậy

$R=\frac{2\sqrt{6} }{3}$

Bài 107158

1 Đáp án

Lý thuyết liên quan

Bài 107158

1 Đáp án

Liên quan

Sử dụng công thức thể tích tính khoảng cách

Lý thuyết liên quan